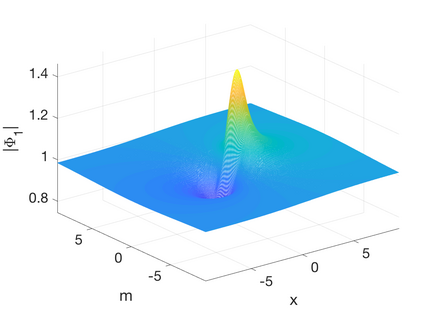
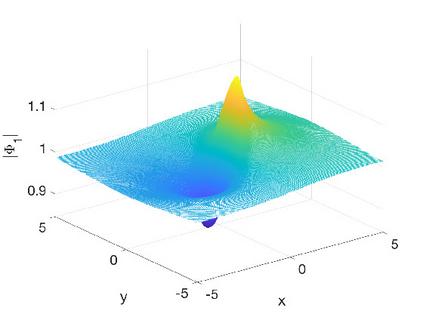
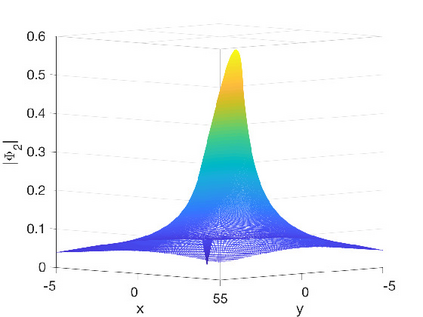
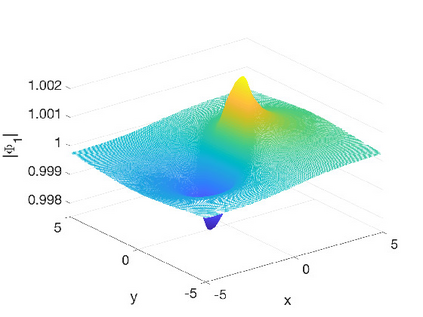
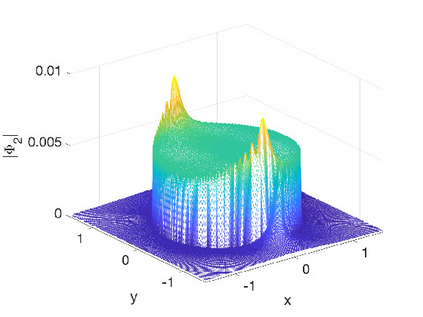
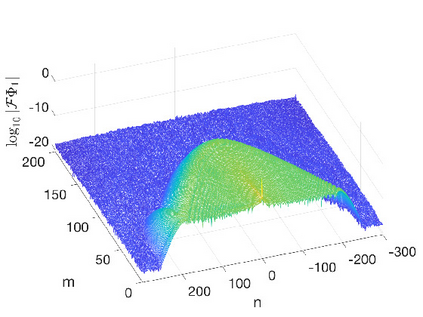
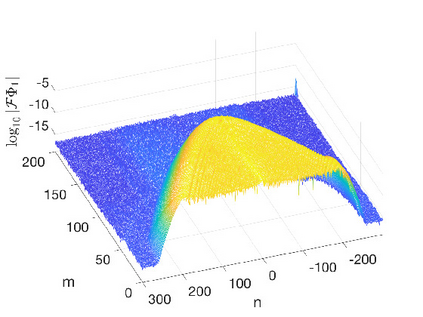
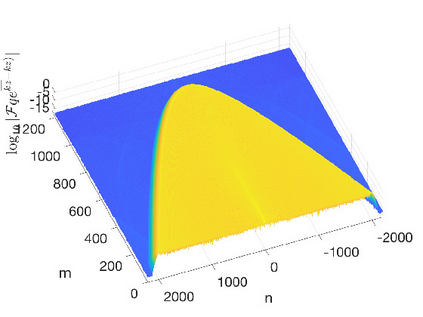
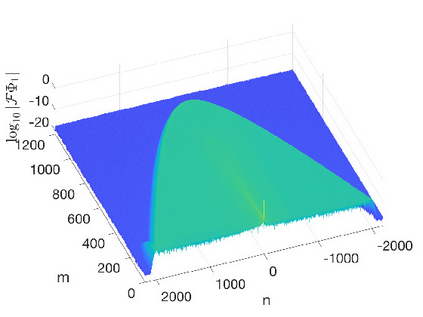
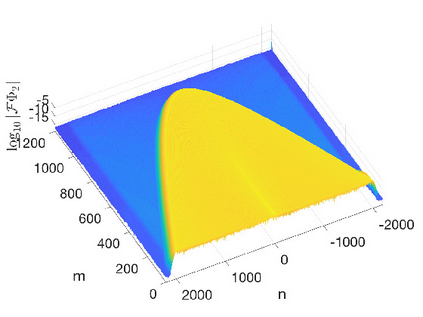
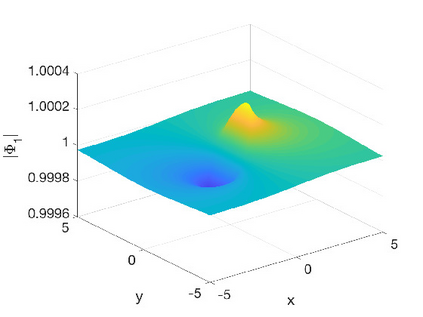
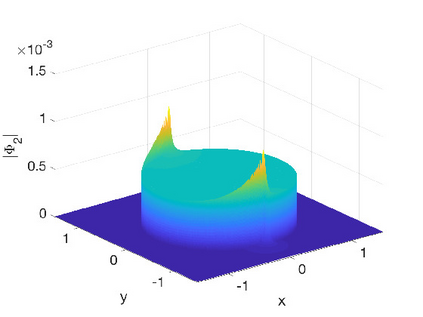
In this work we present spectral algorithms for the numerical scattering for the defocusing Davey-Stewartson (DS) II equation with initial data having compact support on a disk, i.e., for the solution of d-bar problems. Our algorithms use polar coordinates and implement a Chebychev spectral scheme for the radial dependence and a Fourier spectral method for the azimuthal dependence. The focus is placed on the construction of complex geometric optics (CGO) solutions which are needed in the scattering approach for DS. We discuss two different approaches: The first constructs a fundamental solution to the d-bar system and applies the CGO conditions on the latter. This is especially efficient for small values of the modulus of the spectral parameter $k$. The second approach uses a fixed point iteration on a reformulated d-bar system containing the spectral parameter explicitly, a price paid to have simpler asymptotics. The approaches are illustrated for the example of the characteristic function of the disk and are shown to exhibit spectral convergence, i.e., an exponential decay of the numerical error with the number of collocation points. An asymptotic formula for large $|k|$ is given for the reflection coefficient.
翻译:在这项工作中,我们为Davey-Stewartson (DS) II 等式的脱分数提供了光谱算法,其初始数据在磁盘上具有紧凑支持,即用于解决dbar问题。我们的算法使用极坐标,并实施了Chebychev 光谱计划,用于辐射依赖和Azimuthal 依赖的Fourier光谱方法。重点是构建DS 分散方法所需的复杂几何光学(CGO) 解决方案。我们讨论了两种不同的做法:第一种是对dbar 系统构建一个基本解决方案,对dbar 系统应用CGO条件。这对于光谱参数参数的微小值特别有效。第二种方法使用固定的点,用于重订的d-bar 系统,其中明确包含光谱参数,支付的价格更简单一些。为磁盘特性功能的示例展示了两种方法,并展示了光谱融合,即对后者适用CGO条件。对于光谱参数参数的微缩缩缩缩缩缩度值值值值值是用于数值的数值的计算。