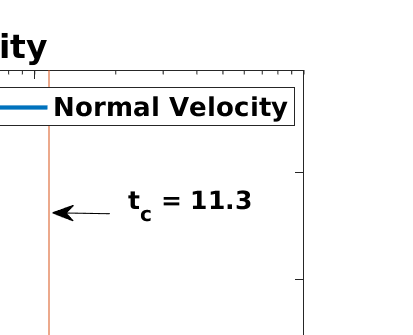
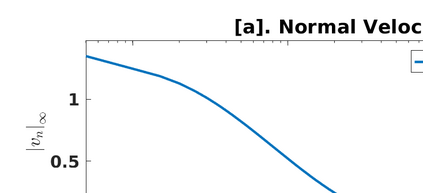
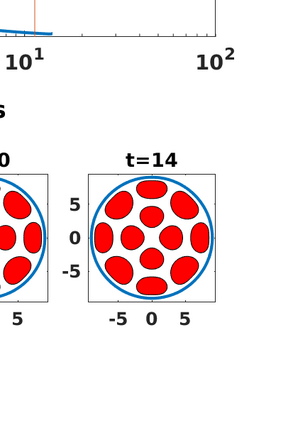
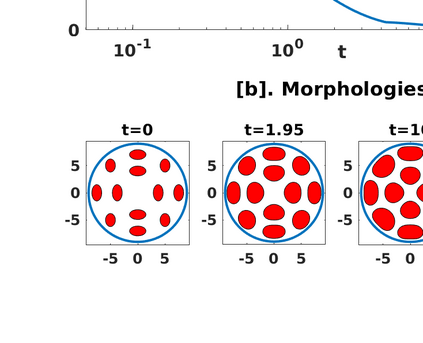
The Ohta-Kawasaki model for diblock-copolymers is well known to the scientific community of diffuse-interface methods. To accurately capture the long-time evolution of the moving interfaces, we present a derivation of the corresponding sharp-interface limit using matched asymptotic expansions, and show that the limiting process leads to a Hele-Shaw type moving interface problem. The numerical treatment of the sharp-interface limit is more complicated due to the stiffness of the equations. To address this problem, we present a boundary integral formulation corresponding to a sharp interface limit of the Ohta-Kawasaki model. Starting with the governing equations defined on separate phase domains, we develop boundary integral equations valid for multi-connected domains in a 2D plane. For numerical simplicity we assume our problem is driven by a uniform Dirichlet condition on a circular far-field boundary. The integral formulation of the problem involves both double- and single-layer potentials due to the modified boundary condition. In particular, our formulation allows one to compute the nonlinear dynamics of a non-equilibrium system and pattern formation of an equilibrating system. Numerical tests on an evolving slightly perturbed circular interface (separating the two phases) are in excellent agreement with the linear analysis, demonstrating that the method is stable, efficient and spectrally accurate in space.
翻译:Ohta- Kawasaki 的二合金聚合物模型是科学界熟知的。为了准确地捕捉移动界面的长期演变过程,我们用匹配的无线扩展来提出相应的尖面限制,并表明限制过程会导致Hel-Shaw类型的移动界面问题。由于方程式的僵硬性,对尖面限制的数值处理更为复杂。为了解决这一问题,我们提出了一个与Ohta-Kawasaki 模型的尖锐界面限制相对应的边界整体配方。从不同阶段域界定的调节方程式开始,我们开发了对多连接域2D平面上有效的边界整体方程式。对于数字简单,我们假设我们的问题是由圆形远处边界的统一Drichlet条件驱动的。问题的整体配方因等式的僵硬性而涉及双层和单层的潜力。特别是,我们的配方可以对非均匀的方格系统的非线性动态进行校准。在双平面平面结构中,对双平面系统进行精确的模拟测试,而平面平面分析的平面分析则进行平稳的平流分析。