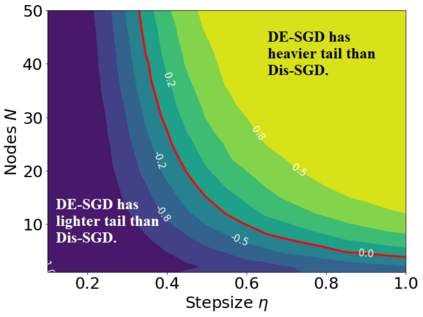
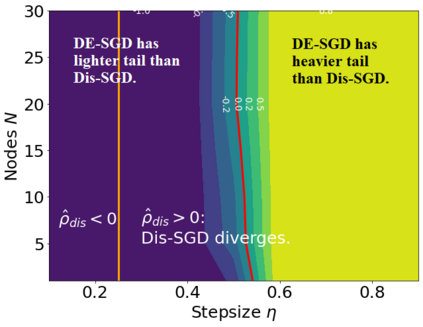
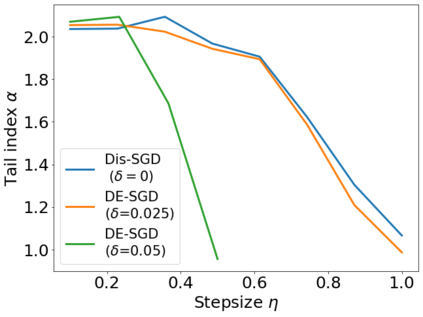
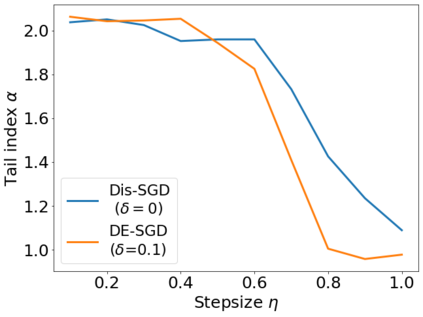
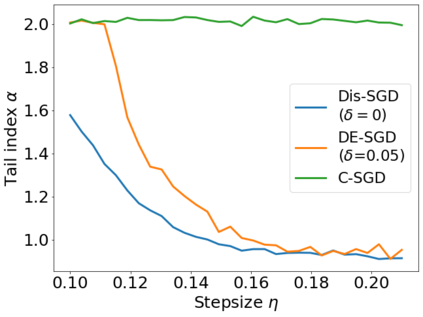
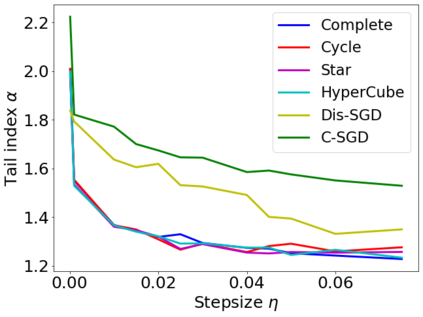
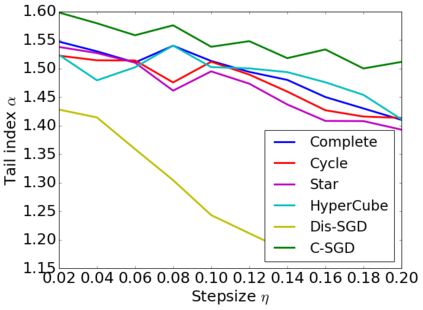
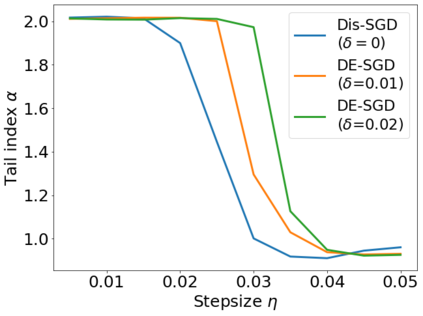
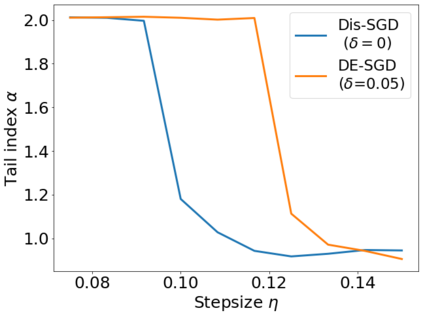
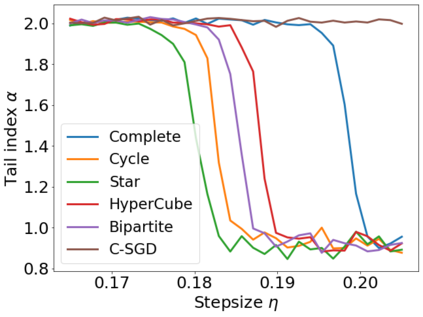
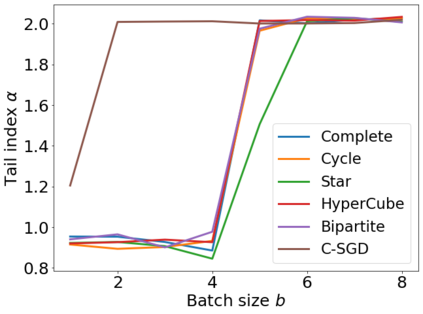
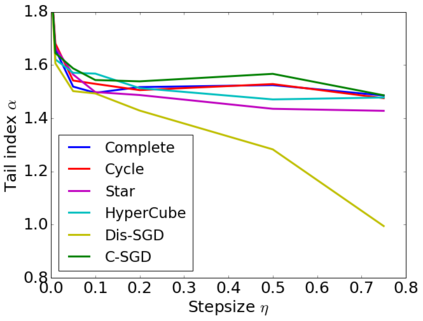
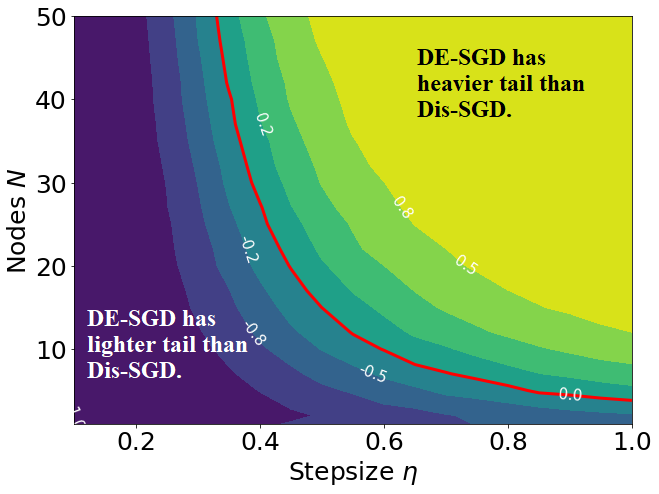
Recent theoretical studies have shown that heavy-tails can emerge in stochastic optimization due to `multiplicative noise', even under surprisingly simple settings, such as linear regression with Gaussian data. While these studies have uncovered several interesting phenomena, they consider conventional stochastic optimization problems, which exclude decentralized settings that naturally arise in modern machine learning applications. In this paper, we study the emergence of heavy-tails in decentralized stochastic gradient descent (DE-SGD), and investigate the effect of decentralization on the tail behavior. We first show that, when the loss function at each computational node is twice continuously differentiable and strongly convex outside a compact region, the law of the DE-SGD iterates converges to a distribution with polynomially decaying (heavy) tails. To have a more explicit control on the tail exponent, we then consider the case where the loss at each node is a quadratic, and show that the tail-index can be estimated as a function of the step-size, batch-size, and the topological properties of the network of the computational nodes. Then, we provide theoretical and empirical results showing that DE-SGD has heavier tails than centralized SGD. We also compare DE-SGD to disconnected SGD where nodes distribute the data but do not communicate. Our theory uncovers an interesting interplay between the tails and the network structure: we identify two regimes of parameters (stepsize and network size), where DE-SGD can have lighter or heavier tails than disconnected SGD depending on the regime. Finally, to support our theoretical results, we provide numerical experiments conducted on both synthetic data and neural networks.
翻译:最近的理论研究表明,由于“ 重复性噪音 ”, 即使是在令人惊讶的简单环境之下, 也会出现重尾, 因为“ 重复性噪音 ”, 即使是在令人惊讶的简单环境之下, 比如高斯数据的线性回归。 虽然这些研究发现了一些有趣的现象, 认为传统的随机性优化问题, 排除了在现代机器学习应用中自然产生的分散性环境。 在本文中, 我们研究分散性随机性梯度下降( DE- SGD) 中出现的重尾尾尾部下降, 并调查权力下放对尾部行为的影响。 我们首先显示, 当每个计算节点的损失函数发生两次连续变化时, 每个计算节点的损耗值会变得更重, 并且更强烈地缩缩缩缩缩在一个区域之外, DESGD 循环法的法律规则会与多组( 重( 重) ) 的分散性优化性优化性优化性优化性调整( SGGD ) 网络的双向更迭性、 双向更深的正变变后, 我们提供更深的理论和深的流数据。