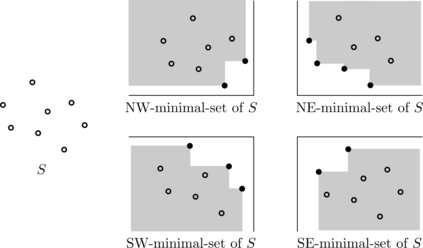
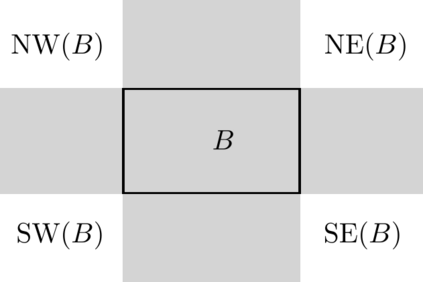
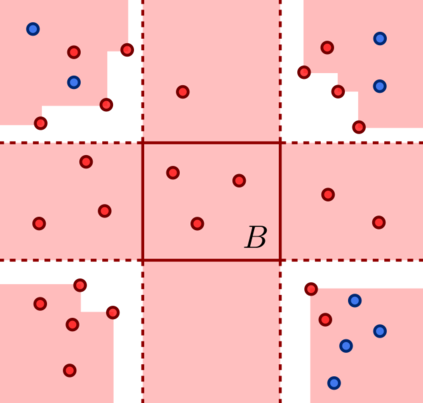
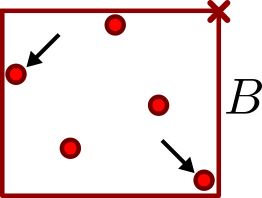
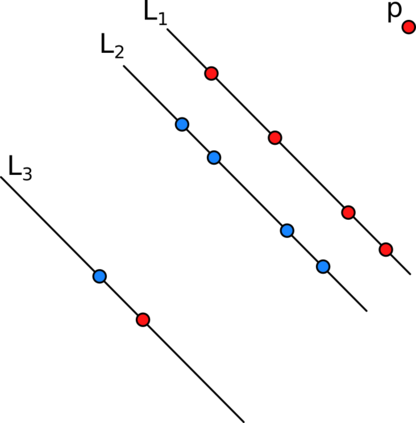
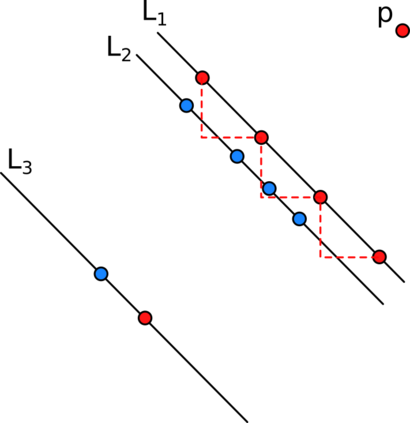
Afshani, Barbay and Chan (2017) introduced the notion of instance-optimal algorithm in the order-oblivious setting. An algorithm A is instance-optimal in the order-oblivious setting for a certain class of algorithms A* if the following hold: - A takes as input a sequence of objects from some domain; - for any instance $\sigma$ and any algorithm A' in A*, the runtime of A on $\sigma$ is at most a constant factor removed from the runtime of A' on the worst possible permutation of $\sigma$. If we identify permutations of a sequence as representing the same instance, this essentially states that A is optimal on every possible input (and not only in the worst case). We design instance-optimal algorithms for the problem of reporting, given a bichromatic set of points in the plane S, all pairs consisting of points of different color which span an empty axis-aligned rectangle (or reporting all points which appear in such a pair). This problem has applications for training-set reduction in nearest-neighbour classifiers. It is also related to the problem consisting of finding the decision boundaries of a euclidean nearest-neighbour classifier, for which Bremner et al. (2005) gave an optimal output-sensitive algorithm. By showing the existence of an instance-optimal algorithm in the order-oblivious setting for this problem we push the methods of Afshani et al. closer to their limits by adapting and extending them to a setting which exhibits highly non-local features. Previous problems for which instance-optimal algorithms were proven to exist were based solely on local relationships between points in a set.
翻译:Afshani, Barbay 和 Chan (2017年) 在排序可见的设置中引入了例式最佳算法的概念。 一种算法 A 是某类算法 A* 的顺序可见设置中的例式最佳算法, 如果以下持有的话 : - 将某域的物体序列作为输入 ; - 在 A* 中, A 的运行时间最多为 A 运行时间的一个不变系数, 从 A 运行时间中从 A 运行时间中去除一个常数, 时间为 $\ sigma$ 的最差的调值 。 如果我们将一个序列的调整确定为同一实例, 这实质上表示 A 是每种可能输入的最优的( 不仅仅是最差的 ) 。 我们设计了用于报告问题的试算法, S 平面图中的所有配法都由不同颜色的点组成, 在空轴对齐的正对角( 或者通过对齐显示所有值显示的精度和最差值值值值的值值值 ) 。 这个问题在最近的平面结构中, 将一个最接近的递解的算方法显示一个更接近的递解的顺序的顺序显示一个更接近的排序。