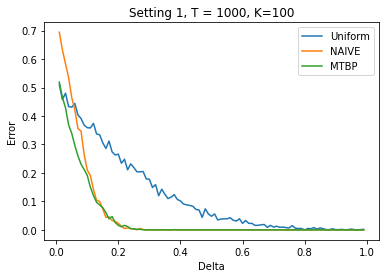
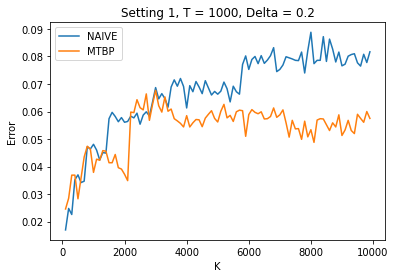
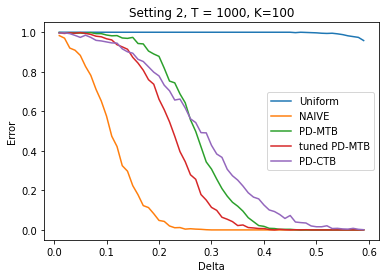
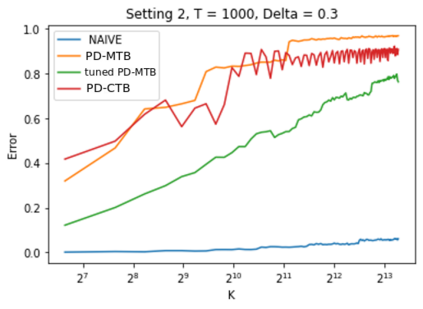
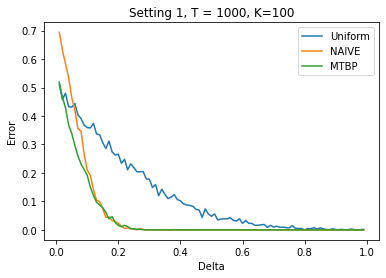
We investigate the problem dependent regime in the stochastic Thresholding Bandit problem (TBP) under several shape constraints. In the TBP, the objective of the learner is to output, at the end of a sequential game, the set of arms whose means are above a given threshold. The vanilla, unstructured, case is already well studied in the literature. Taking $K$ as the number of arms, we consider the case where (i) the sequence of arm's means $(\mu_k)_{k=1}^K$ is monotonically increasing (MTBP) and (ii) the case where $(\mu_k)_{k=1}^K$ is concave (CTBP). We consider both cases in the problem dependent regime and study the probability of error - i.e. the probability to mis-classify at least one arm. In the fixed budget setting, we provide upper and lower bounds for the probability of error in both the concave and monotone settings, as well as associated algorithms. In both settings the bounds match in the problem dependent regime up to universal constants in the exponential.
翻译:在TBP中,学习者的目标是在连续游戏结束时输出其手段超过某一阈值的一组武器。在文献中已经对香草、无结构的病例进行了深入研究。用K$作为武器数量,我们考虑的情况是:(一) 手臂的顺序在单质增加(MTBP)和(二) $(mu_k)k=1K$的情况下,学习者的目标是在连续游戏结束时输出其手段超过某一阈值的一组武器。我们考虑两种情况,研究错误的可能性――即至少一个手臂的分类错误的可能性。在固定的预算设置中,我们提供上下限,说明在连接和单调环境中发生错误的可能性,以及相关的算法。在两种情况下,问题依赖制度的界限都与指数中的普遍常数相符。