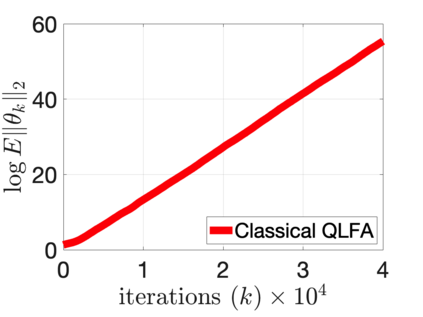
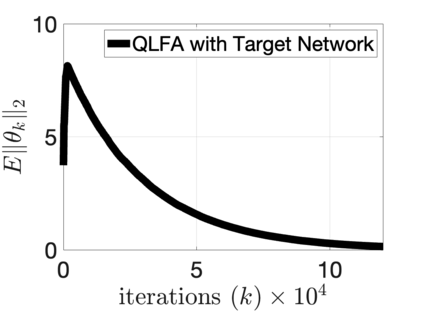
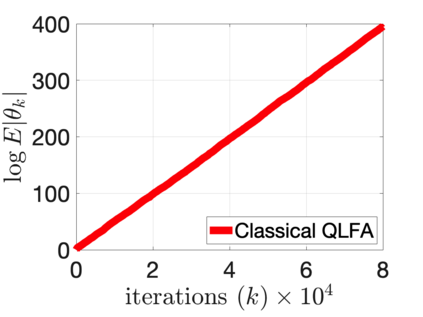
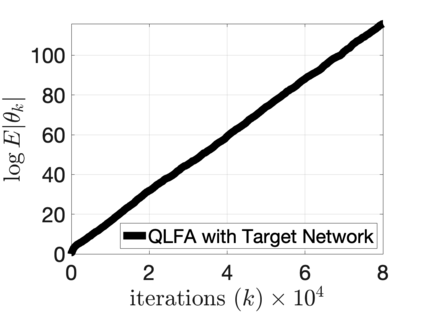
$Q$-learning with function approximation is one of the most empirically successful while theoretically mysterious reinforcement learning (RL) algorithms, and was identified in Sutton (1999) as one of the most important theoretical open problems in the RL community. Even in the basic linear function approximation setting, there are well-known divergent examples. In this work, we show that \textit{target network} and \textit{truncation} together are enough to provably stabilize $Q$-learning with linear function approximation, and we establish the finite-sample guarantees. The result implies an $O(\epsilon^{-2})$ sample complexity up to a function approximation error. Moreover, our results do not require strong assumptions or modifying the problem parameters as in existing literature.
翻译:以函数近似值学习Q$是经验上最成功的之一,而理论上神秘的强化学习算法(RL)在理论上最为成功,在Sutton(1999年)中被确定为RL社区最重要的理论开放问题之一。即使在基本的线性函数近似设置中,也有众所周知的不同例子。在这项工作中,我们显示\ textit{目标网络}和\textit{truit{truncation}合在一起足以用线性函数近似来稳定$Q$的学习,而我们则建立了有限抽样保证。结果意味着在功能近似误差之前,样本复杂度为$O( epsilon}-2})$。此外,我们的结果并不需要强有力的假设或修改现有文献中的问题参数。