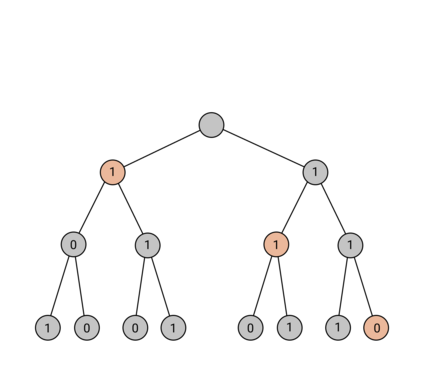
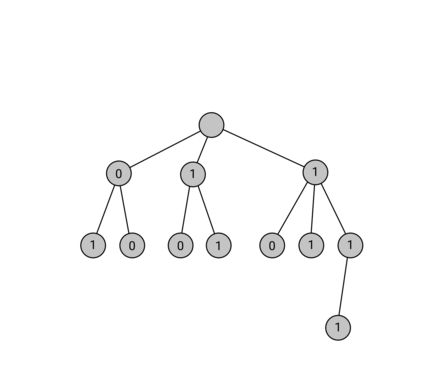
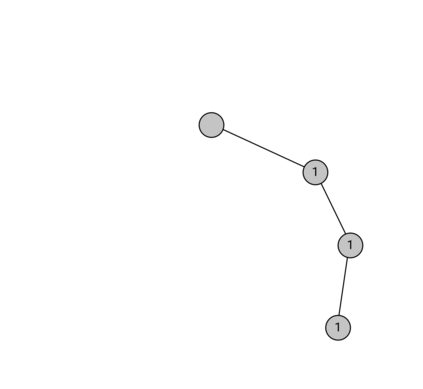
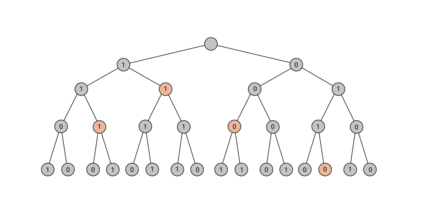
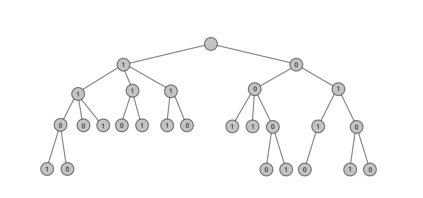
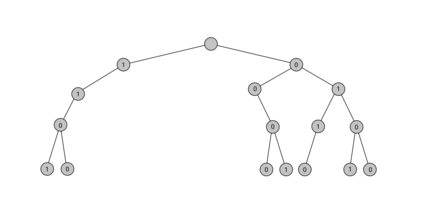
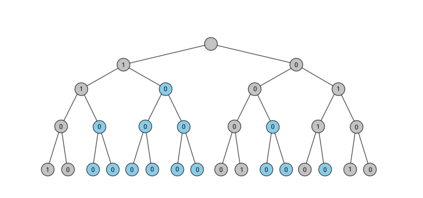
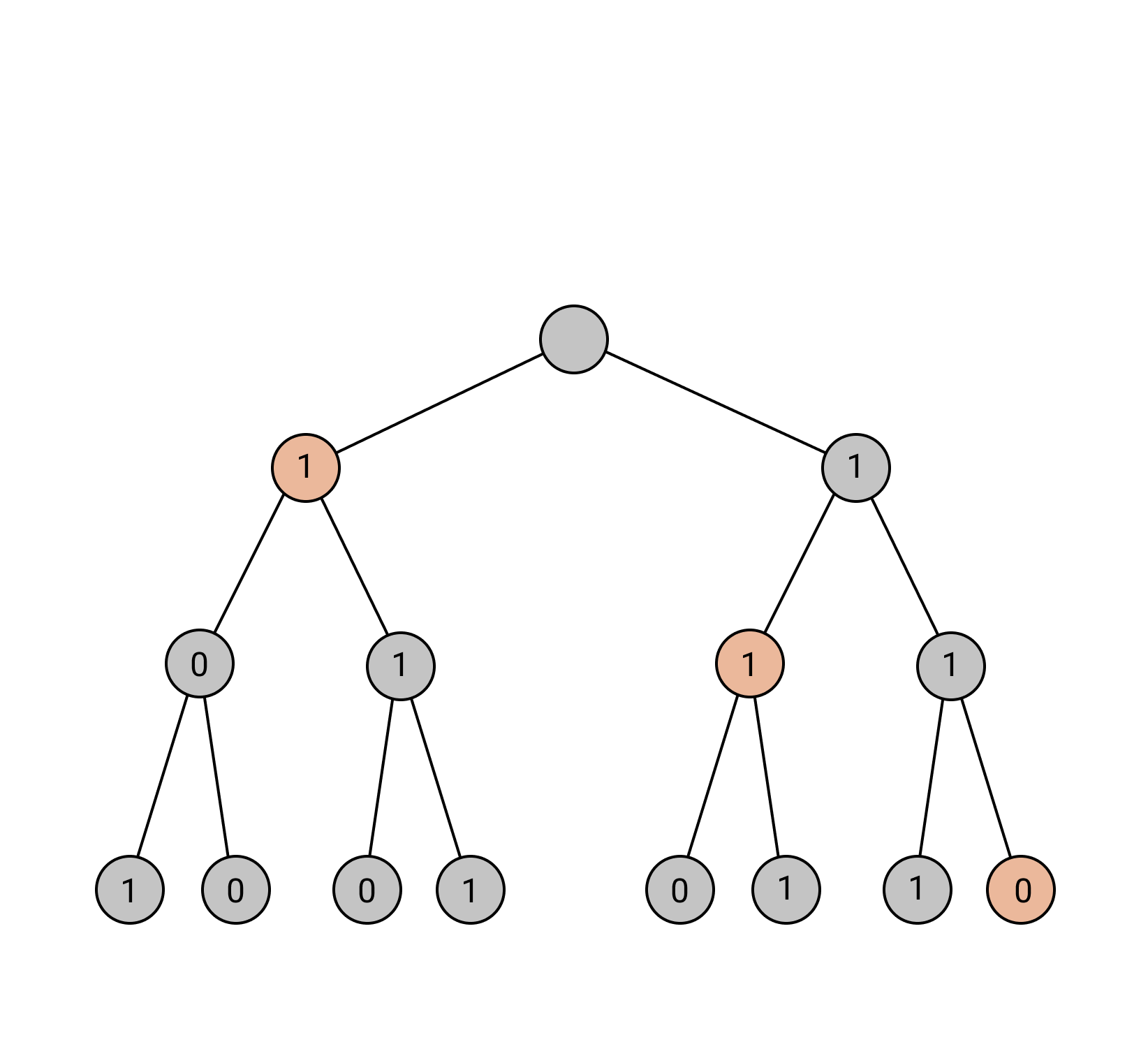
Tree trace reconstruction aims to learn the binary node labels of a tree, given independent samples of the tree passed through an appropriately defined deletion channel. In recent work, Davies, R\'acz, and Rashtchian used combinatorial methods to show that $\exp(\mathcal{O}(k \log_{k} n))$ samples suffice to reconstruct a complete $k$-ary tree with $n$ nodes with high probability. We provide an alternative proof of this result, which allows us to generalize it to a broader class of tree topologies and deletion models. In our proofs, we introduce the notion of a subtrace, which enables us to connect with and generalize recent mean-based complex analytic algorithms for string trace reconstruction.
翻译:树痕重建旨在学习树的二元节点标签, 给通过一个定义得当的删除渠道传递的树的独立样本。 在最近的工作中, Davies, R\'acz 和 Rashtchian 使用组合方法来显示$\ exp( mathcal{O})( k\log ⁇ k} n) 的样本足以用高概率的 $n 节点重建完整的一棵$k$ 的树。 我们为这一结果提供了一个替代证明, 这使得我们可以将其概括为更广泛的树本和删除模型。 在我们的证明中, 我们引入了子轨道的概念, 从而使我们能够连接和概括最近基于平均的复杂分析算法, 用于字符串跟踪重建 。