On Feature Collapse and Deep Kernel Learning for Single Forward Pass Uncertainty

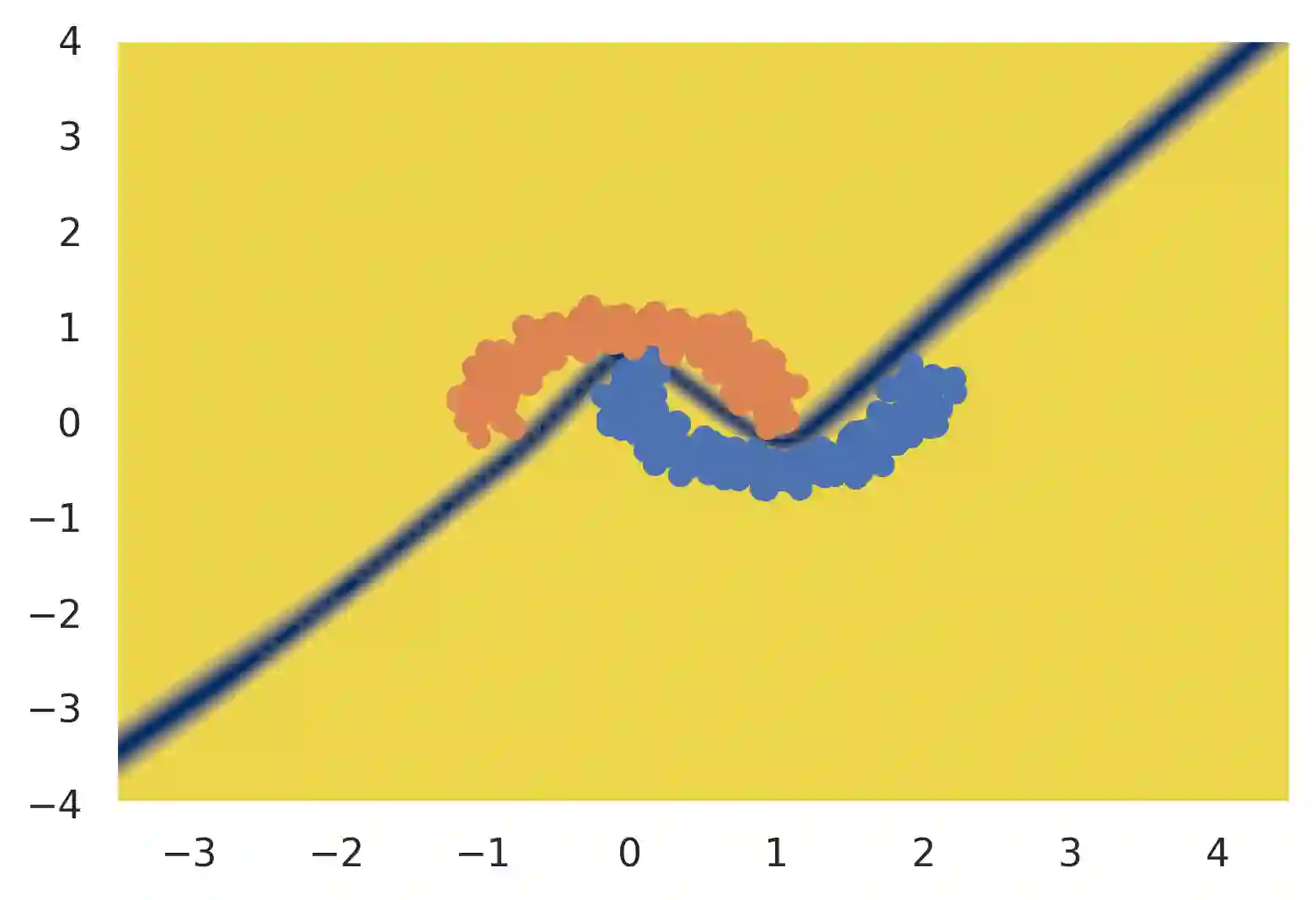
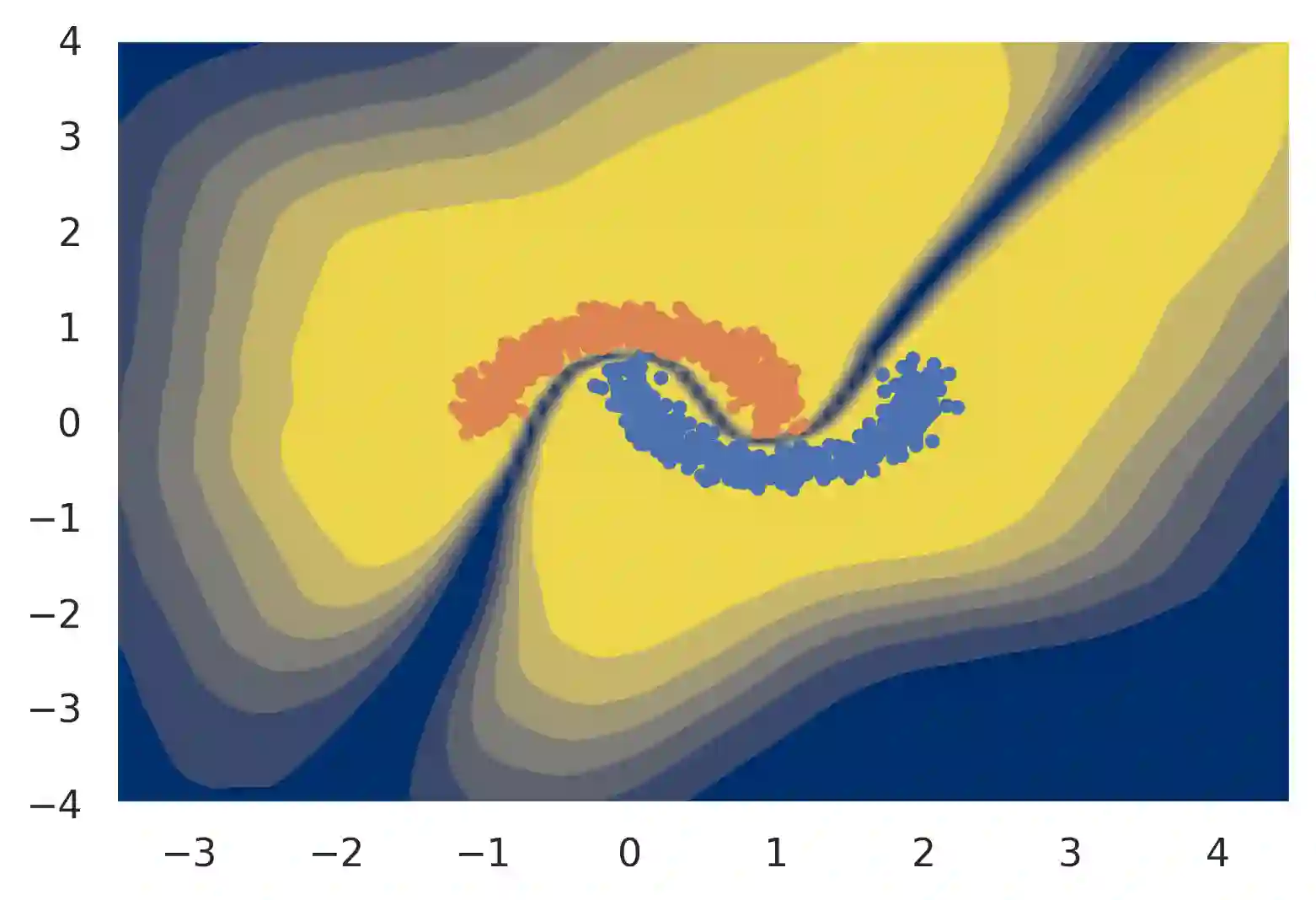
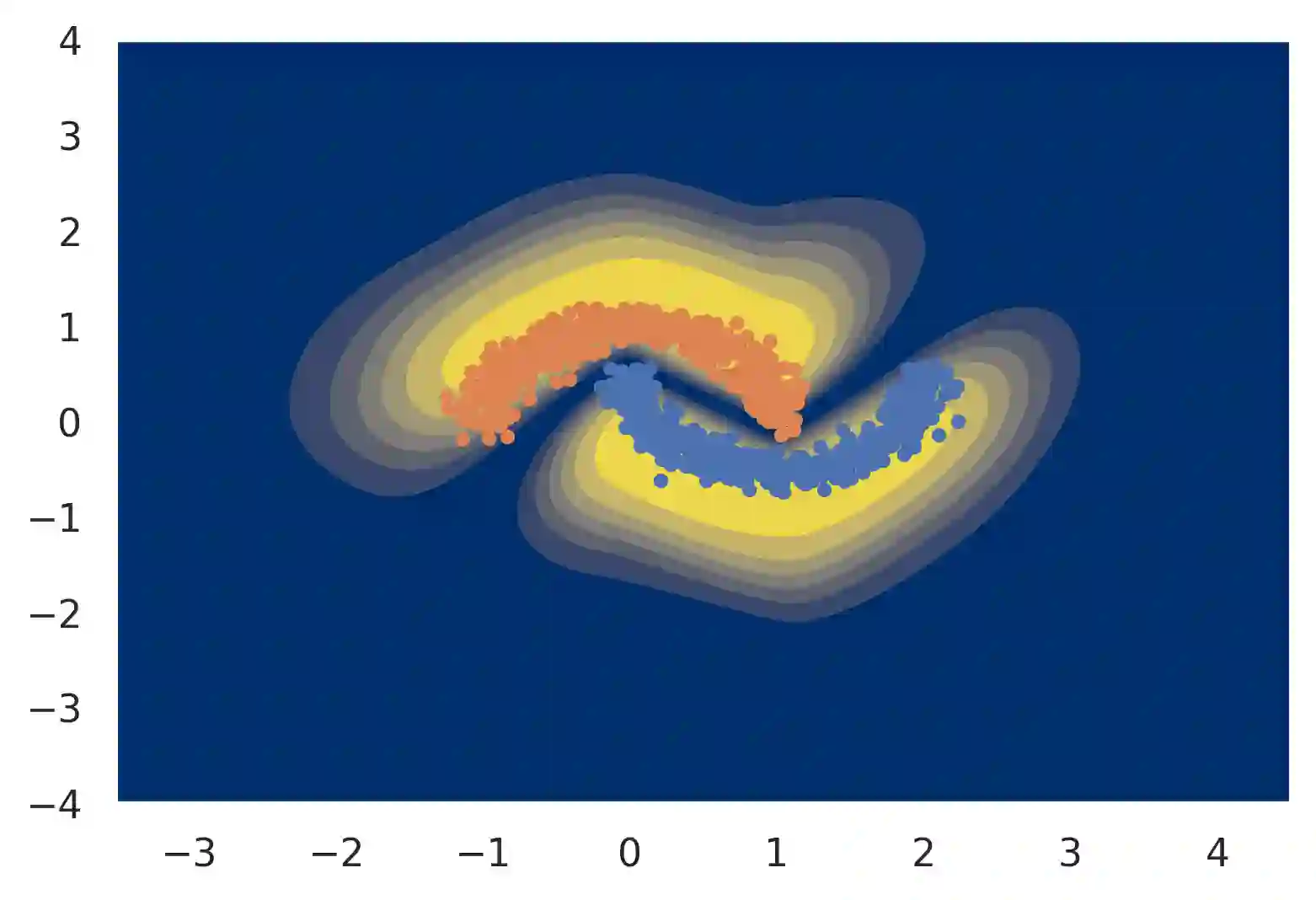
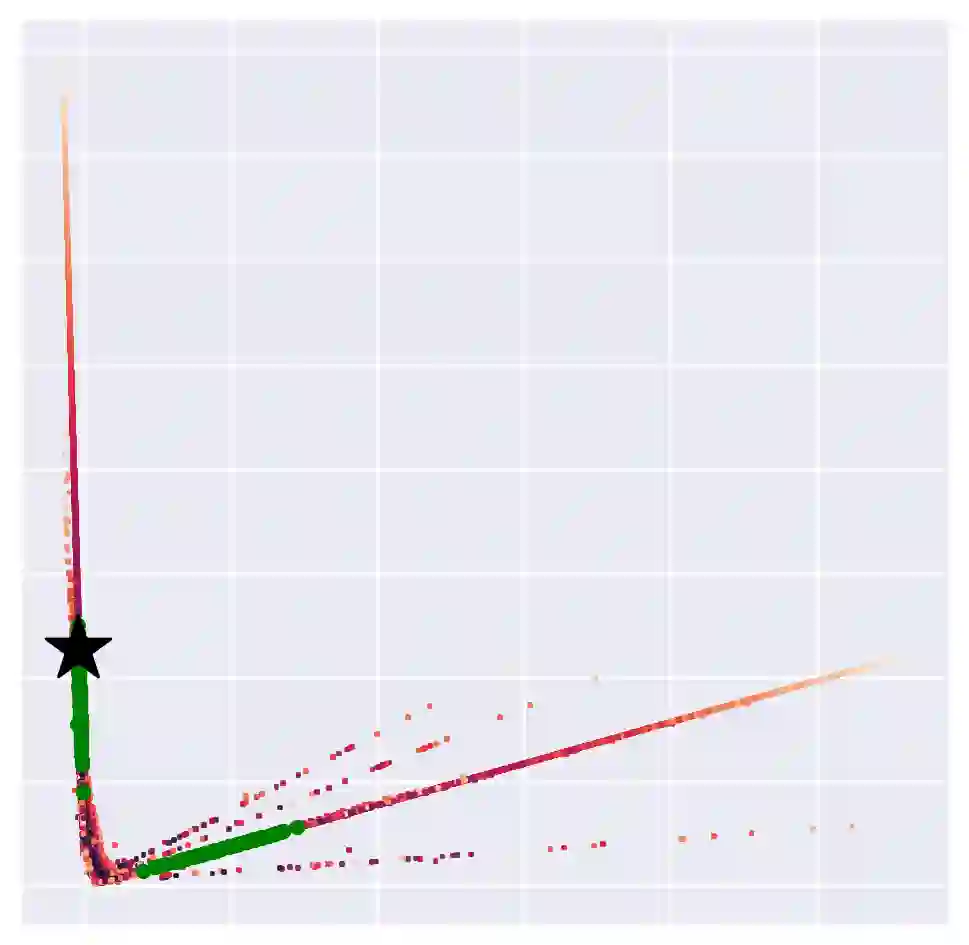
Gaussian processes are often considered a gold standard in uncertainty estimation with low dimensional data, but they have difficulty scaling to high dimensional inputs. Deep Kernel Learning (DKL) was introduced as a solution to this problem: a deep feature extractor is used to transform the inputs over which a Gaussian process' kernel is defined. However, DKL has been shown to provide unreliable uncertainty estimates in practice. We study why, and show that for certain feature extractors, "far-away" data points are mapped to the same features as those of training-set points. With this insight we propose to constrain DKL's feature extractor to approximately preserve distances through a bi-Lipschitz constraint, resulting in a feature space favorable to DKL. We obtain a model, DUE, which demonstrates uncertainty quality outperforming previous DKL and single forward pass uncertainty methods, while maintaining the speed and accuracy of softmax neural networks.