Private Matrix Multiplication From MDS-Coded Storage With Colluding Servers

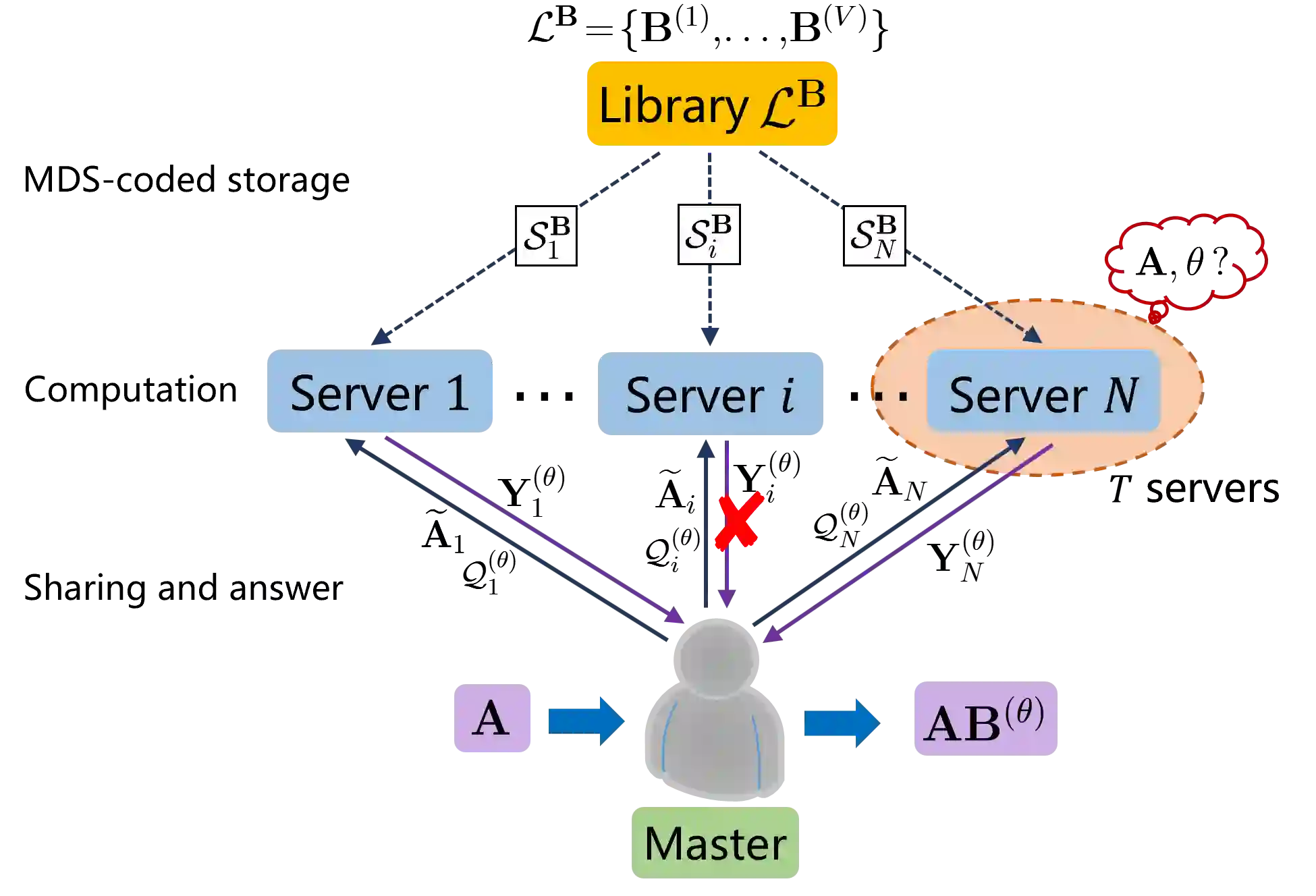
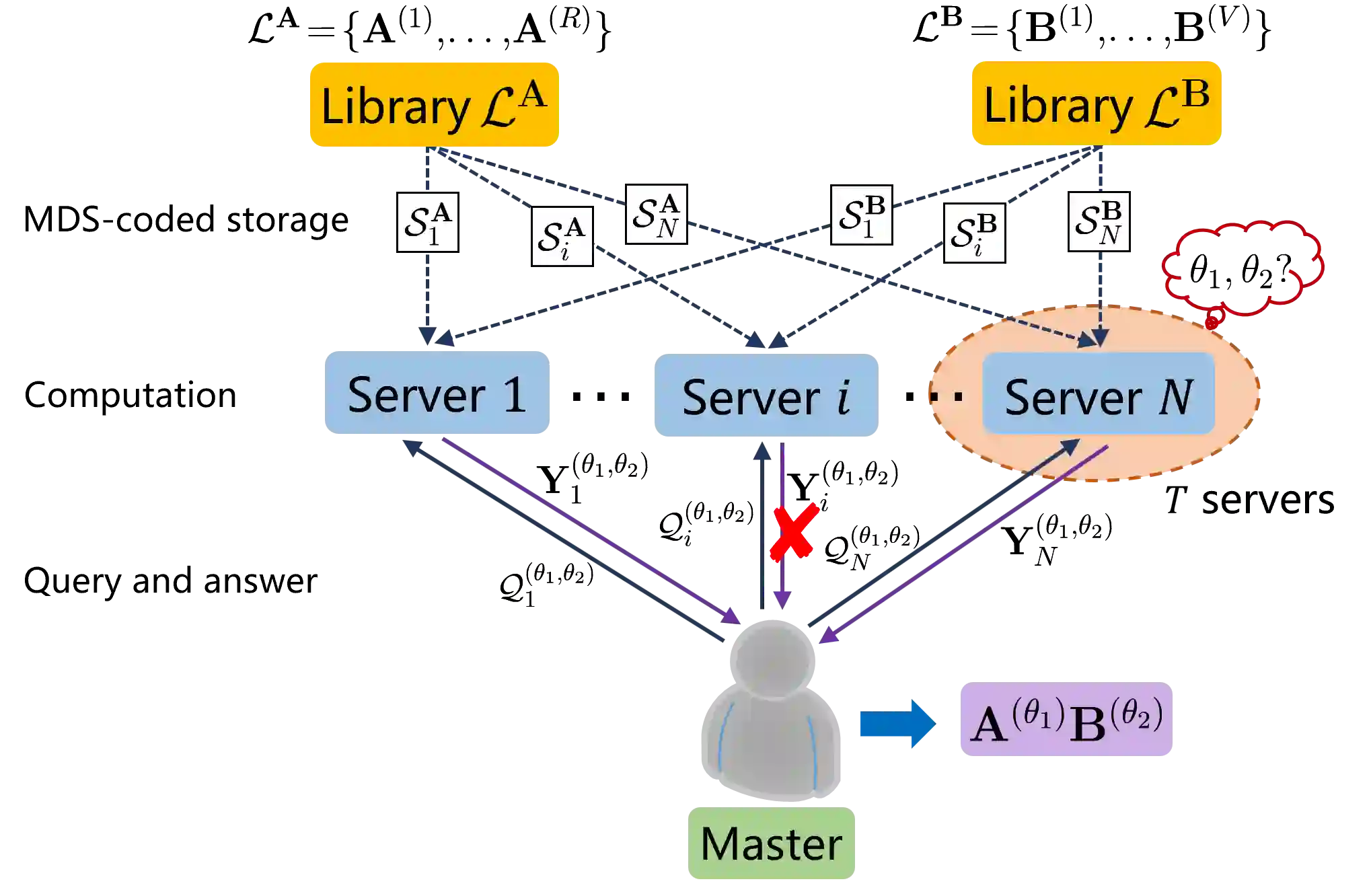
In this paper, we study the two problems of Private and Secure Matrix Multiplication and Fully Private Matrix Multiplication from MDS-coded storage with Colluding servers, referred to as MDS-C-PSMM and MDS-C-FPMM respectively, on a distributed computing system with a master node and multiple servers. Specifically, in the MDS-C-PSMM problem, the master wants to compute the product of its owned confidential matrix $\mathbf{A}$ with one out of a batch of public matrices that is stored across distributed servers according to an MDS code, without revealing any information about the matrix $\mathbf{A}$ and the index of another interested matrix to a certain number of colluding servers. In the second MDS-C-FPMM problem, the matrix $\mathbf{A}$ is also selected from another batch of public matrices that is stored at the servers in MDS-coded form. In this case, the indices of the two interested matrices should be kept private from the colluding servers. We construct computation strategies for both MDS-C-PSMM and MDS-C-FPMM problems by exploiting the structure inspired by the encoding functions of related secure matrix multiplication strategies, yielding flexible tradeoffs among recovery threshold, i.e., the number of servers required to recover desired product, computation overhead, i.e., the computation complexity of distributed system, and communication overhead, i.e., the amount of communication bits between the master and the servers.