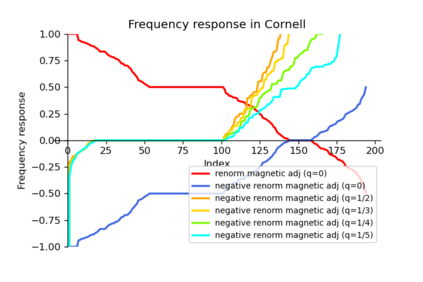
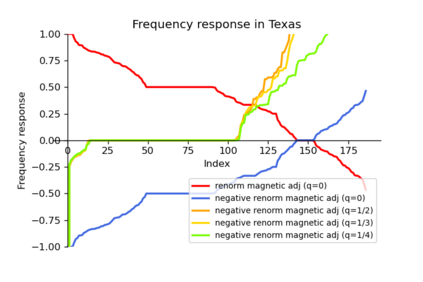
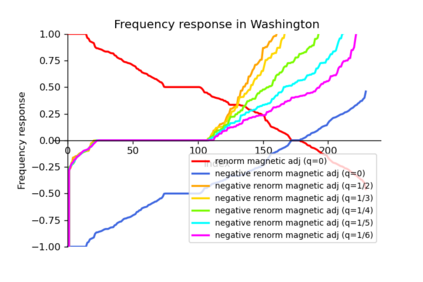
Recent advancements in Graph Neural Networks have led to state-of-the-art performance on graph representation learning. However, the majority of existing works process directed graphs by symmetrization, which causes loss of directional information. To address this issue, we introduce the magnetic Laplacian, a discrete Schr\"odinger operator with magnetic field, which preserves edge directionality by encoding it into a complex phase with an electric charge parameter. By adopting a truncated variant of PageRank named Linear- Rank, we design and build a low-pass filter for homogeneous graphs and a high-pass filter for heterogeneous graphs. In this work, we propose a complex-valued graph convolutional network named Magnetic Graph Convolutional network (MGC). With the corresponding complex-valued techniques, we ensure our model will be degenerated into real-valued when the charge parameter is in specific values. We test our model on several graph datasets including directed homogeneous and heterogeneous graphs. The experimental results demonstrate that MGC is fast, powerful, and widely applicable.
翻译:图表神经网络最近的进展导致在图形显示学习方面最先进的性能。 但是,大多数现有的工程过程都通过对称化来引导图形,从而导致方向信息丢失。为了解决这一问题,我们引入了磁场磁拉平相,一个离散的Schr\'doninger操作器,它通过将电荷参数编码成一个复杂阶段来保持边缘方向性。我们采用名为PageRank的直线级的截断变体,设计和建造了一个用于同质图形的低通道过滤器,以及一个用于多式图形的高通路过滤器。在这项工作中,我们提出了一个名为磁电动图动网络(MGC)的复杂价值的平流图网络。在相应的复杂价值技术下,我们确保我们的模型在充电参数为特定值时会变成真实价值。我们用几个图形数据集测试我们的模型,包括定向的同质和多式图表。实验结果表明,MGC是快速、强大和可广泛应用的。