Robustness to Label Noise Depends on the Shape of the Noise Distribution in Feature Space

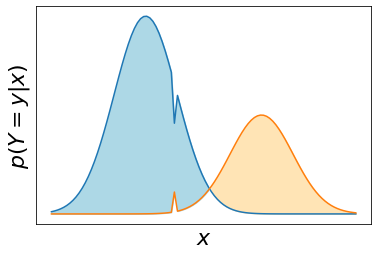
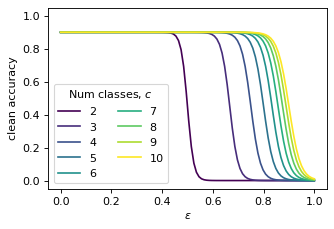
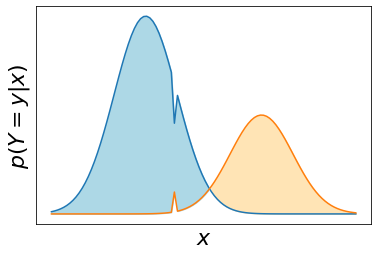
Machine learning classifiers have been demonstrated, both empirically and theoretically, to be robust to label noise under certain conditions -- notably the typical assumption is that label noise is independent of the features given the class label. We provide a theoretical framework that generalizes beyond this typical assumption by modeling label noise as a distribution over feature space. We show that both the scale and the shape of the noise distribution influence the posterior likelihood; and the shape of the noise distribution has a stronger impact on classification performance if the noise is concentrated in feature space where the decision boundary can be moved. For the special case of uniform label noise (independent of features and the class label), we show that the Bayes optimal classifier for $c$ classes is robust to label noise until the ratio of noisy samples goes above $\frac{c-1}{c}$ (e.g. 90% for 10 classes), which we call the tipping point. However, for the special case of class-dependent label noise (independent of features given the class label), the tipping point can be as low as 50%. Most importantly, we show that when the noise distribution targets decision boundaries (label noise is directly dependent on feature space), classification robustness can drop off even at a small scale of noise. Even when evaluating recent label-noise mitigation methods we see reduced accuracy when label noise is dependent on features. These findings explain why machine learning often handles label noise well if the noise distribution is uniform in feature-space; yet it also points to the difficulty of overcoming label noise when it is concentrated in a region of feature space where a decision boundary can move.