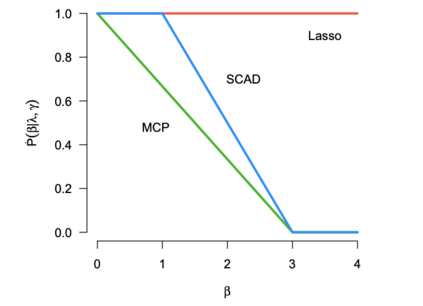
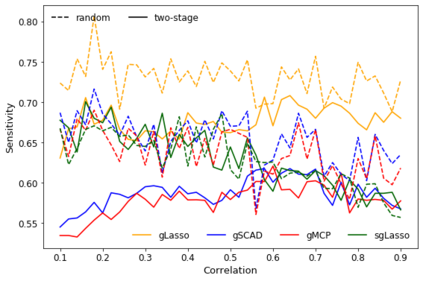
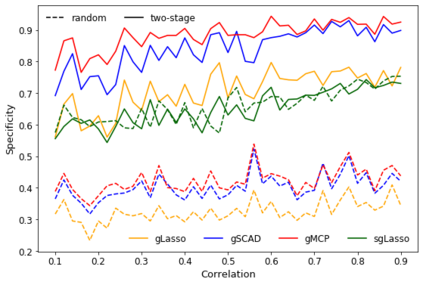
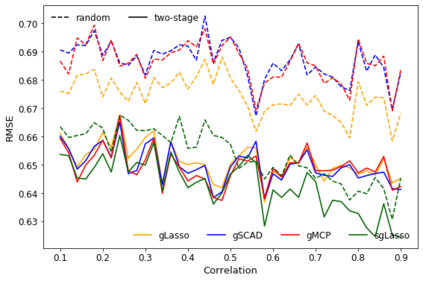
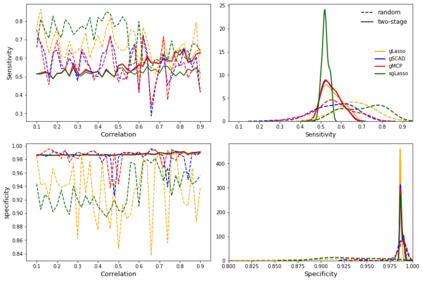
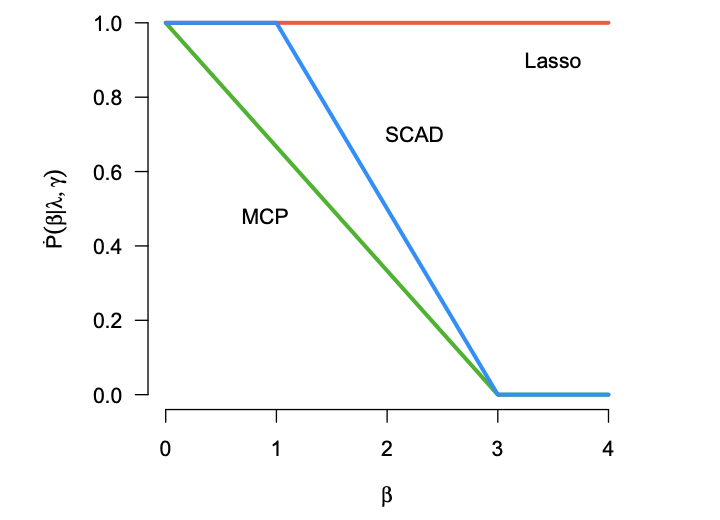
When fitting statistical models, some predictors are often found to be correlated with each other, and functioning together. Many group variable selection methods are developed to select the groups of predictors that are closely related to the continuous or categorical response. These existing methods usually assume the group structures are well known. For example, variables with similar practical meaning, or dummy variables created by categorical data. However, in practice, it is impractical to know the exact group structure, especially when the variable dimensional is large. As a result, the group variable selection results may be selected. To solve the challenge, we propose a two-stage approach that combines a variable clustering stage and a group variable stage for the group variable selection problem. The variable clustering stage uses information from the data to find a group structure, which improves the performance of the existing group variable selection methods. For ultrahigh dimensional data, where the predictors are much larger than observations, we incorporated a variable screening method in the first stage and shows the advantages of such an approach. In this article, we compared and discussed the performance of four existing group variable selection methods under different simulation models, with and without the variable clustering stage. The two-stage method shows a better performance, in terms of the prediction accuracy, as well as in the accuracy to select active predictors. An athlete's data is also used to show the advantages of the proposed method.
翻译:当适当的统计模型时,往往发现某些预测者彼此关联,并同时发挥作用。许多组的可变选择方法是用来选择与连续或绝对响应密切相关的预测者组的。这些现有方法通常假定群结构是众所周知的。例如,具有类似实际含义的变量,或由绝对数据创造的假变量。然而,在实践中,了解确切的群组结构是不切实际的,特别是当变量的维度很大时。因此,可以选择组的可变选择结果。为了解决挑战,我们建议了一种两阶段办法,即结合一个可变群群集阶段和组的可变阶段来选择群变量选择问题。变量组合阶段利用数据中的信息来寻找组结构,从而改进现有群群变量选择方法的性能。对于超高的天体数据,如果预测者比观察者大得多,我们在第一阶段就采用了变量筛选方法,并展示了这种方法的优点。在本条中,我们比较并讨论了不同模拟模型中四种现有组的可变组选择方法的性能,在可变组组的组组选择阶段和不具有可变组选择的精确性。两阶段方法也显示了用于预测的精确性,在预测方法中,以显示主动性数据的精确性方法的精确性。在所选为预的精确性。