VectorTSP: A Traveling Salesperson Problem with Racetrack-like acceleration constraints

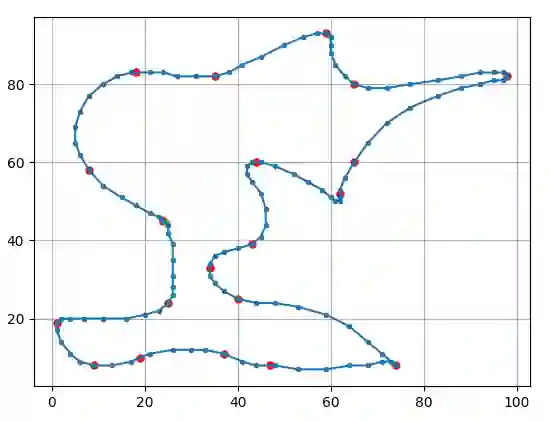
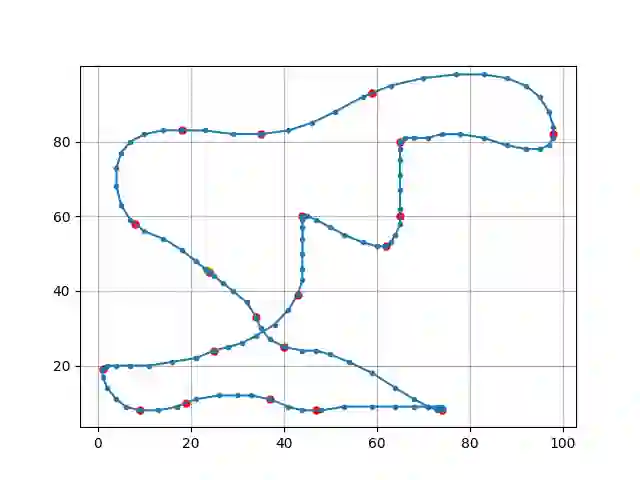
We study a new version of the Euclidean TSP called VectorTSP (VTSP for short) where a mobile entity is allowed to move according to a set of physical constraints inspired from the pen-and-pencil game Racetrack (also known as Vector Racer ). In contrast to other versions of TSP accounting for physical constraints, such as Dubins TSP, the spirit of this model is that (1) no speed limitations apply, and (2) inertia depends on the current velocity. As such, this model is closer to typical models considered in path planning problems, although applied here to the visit of n cities in a non-predetermined order. We motivate and introduce the VectorTSP problem, discussing fundamental differences with previous versions of TSP. In particular, an optimal visit order for ETSP may not be optimal for VTSP. We show that VectorTSP is NP-hard, and in the other direction, that VectorTSP reduces to GroupTSP in polynomial time (although with a significant blow-up in size). On the algorithmic side, we formulate the search for a solution as an interactive scheme between a high-level algorithm and a trajectory oracle, the former being responsible for computing the visit order and the latter for computing the cost (or the trajectory) for a given visit order. We present algorithms for both, and we demonstrate and quantify through experiments that this approach frequently finds a better solution than the optimal trajectory realizing an optimal ETSP tour, which legitimates the problem itself and (we hope) motivates further algorithmic developments.