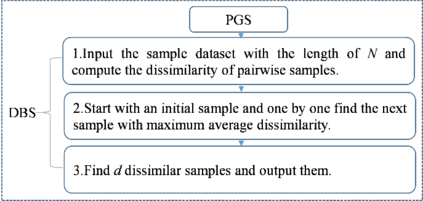
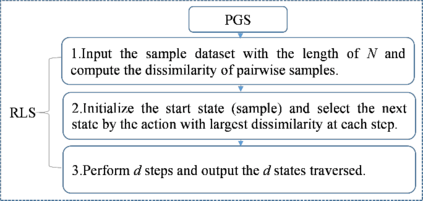
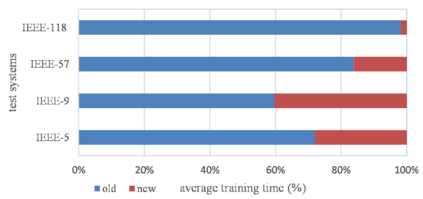
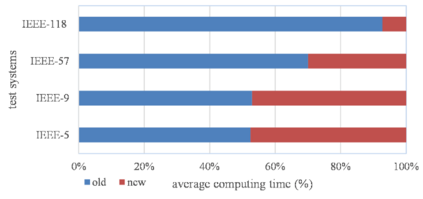
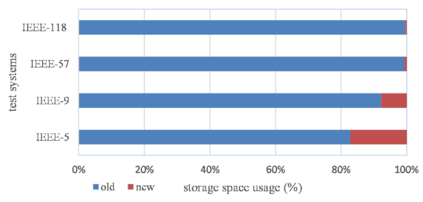
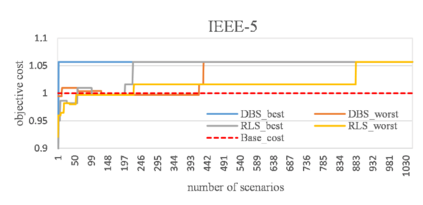
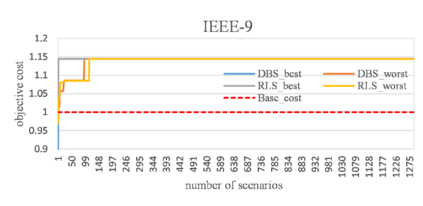
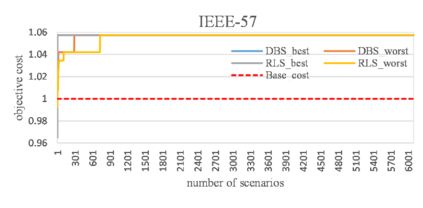
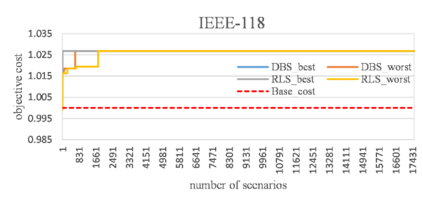
The multi-period dynamics of energy storage (ES), intermittent renewable generation and uncontrollable power loads, make the optimization of power system operation (PSO) challenging. A multi-period optimal PSO under uncertainty is formulated using the chance-constrained optimization (CCO) modeling paradigm, where the constraints include the nonlinear energy storage and AC power flow models. Based on the emerging scenario optimization method which does not rely on pre-known probability distribution functions, this paper develops a novel solution method for this challenging CCO problem. The proposed meth-od is computationally effective for mainly two reasons. First, the original AC power flow constraints are approximated by a set of learning-assisted quadratic convex inequalities based on a generalized least absolute shrinkage and selection operator. Second, considering the physical patterns of data and motived by learning-based sampling, the strategic sampling method is developed to significantly reduce the required number of scenarios through different sampling strategies. The simulation results on IEEE standard systems indicate that 1) the proposed strategic sampling significantly improves the computational efficiency of the scenario-based approach for solving the chance-constrained optimal PSO problem, 2) the data-driven convex approximation of power flow can be promising alternatives of nonlinear and nonconvex AC power flow.
翻译:能源储存、间歇性可再生发电和无法控制的电力负荷的多周期动态能源储存、间歇性可再生能源发电和多周期性电荷的动态,使得优化电力系统运行具有挑战性。在不确定情况下,利用机会限制的优化模型模式(CCO)制定多周期最佳的PSO, 其制约因素包括非线性能源储存和AC电力流模型。根据不依赖预先知道的概率分布功能的新兴情景优化方法,本文件为这一具有挑战性的CO2问题开发了一种新的解决方案方法。提议的甲基水在计算上非常有效,原因主要有两个。首先,最初的AC电力流量限制因一套学习辅助的象形锥体不平等而近似于一套基于普遍最低绝对收缩和选择操作者的学习辅助二次模型。第二,考虑到数据的实际模式和基于学习抽样的动机,正在开发战略取样方法,以通过不同的取样战略大大减少所需假设情况的数量。IEEE标准系统的模拟结果表明,1,拟议的战略取样大大改进了基于假设的方法的计算效率,以解决机会限制最佳的PSOx动力流非动力流的动力流的模型。