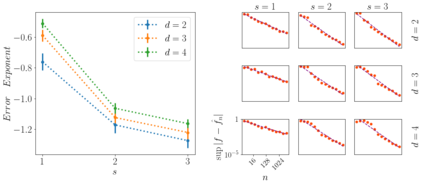
An interesting observation in artificial neural networks is their favorable generalization error despite typically being extremely overparameterized. It is well known that the classical statistical learning methods often result in vacuous generalization errors in the case of overparameterized neural networks. Adopting the recently developed Neural Tangent (NT) kernel theory, we prove uniform generalization bounds for overparameterized neural networks in kernel regimes, when the true data generating model belongs to the reproducing kernel Hilbert space (RKHS) corresponding to the NT kernel. Importantly, our bounds capture the exact error rates depending on the differentiability of the activation functions. In order to establish these bounds, we propose the information gain of the NT kernel as a measure of complexity of the learning problem. Our analysis uses a Mercer decomposition of the NT kernel in the basis of spherical harmonics and the decay rate of the corresponding eigenvalues. As a byproduct of our results, we show the equivalence between the RKHS corresponding to the NT kernel and its counterpart corresponding to the Mat\'ern family of kernels, showing the NT kernels induce a very general class of models. We further discuss the implications of our analysis for some recent results on the regret bounds for reinforcement learning and bandit algorithms, which use overparameterized neural networks.
翻译:在人工神经网络中,一个有趣的观察是,人工神经网络的偏好一般化错误,尽管通常被过分过度分化。众所周知,古典统计学习方法往往导致在超分度神经网络中出现失常的泛化错误。采用最近开发的神经内核(NT)内核理论,我们证明在内核系统中,当真正的数据生成模型属于与NT内核相对应的再生产内核Hilbert空间(RKHS)的衰变率时,对超分神经网络来说是一致的。重要的是,我们的界限根据激活功能的可变性来捕捉准确的错误率。为了建立这些界限,我们建议将NT内核的增益作为衡量学习问题复杂性的尺度。我们的分析利用了NT内核内核网络在NT内核和对等值的等值之间的等同度,我们用LKHS网络对NT内核的内核和对等值的内核分析,我们用NT内核内核的内核的内核的内核对等值来进一步解释。