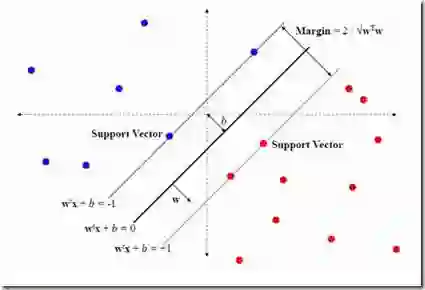
We present a quantum interior-point method (IPM) for second-order cone programming (SOCP) that runs in time $\widetilde{O} \left( n\sqrt{r} \frac{\zeta \kappa}{\delta^2} \log \left(1/\epsilon\right) \right)$ where $r$ is the rank and $n$ the dimension of the SOCP, $\delta$ bounds the distance of intermediate solutions from the cone boundary, $\zeta$ is a parameter upper bounded by $\sqrt{n}$, and $\kappa$ is an upper bound on the condition number of matrices arising in the classical IPM for SOCP. The algorithm takes as its input a suitable quantum description of an arbitrary SOCP and outputs a classical description of a $\delta$-approximate $\epsilon$-optimal solution of the given problem. Furthermore, we perform numerical simulations to determine the values of the aforementioned parameters when solving the SOCP up to a fixed precision $\epsilon$. We present experimental evidence that in this case our quantum algorithm exhibits a polynomial speedup over the best classical algorithms for solving general SOCPs that run in time $O(n^{\omega+0.5})$ (here, $\omega$ is the matrix multiplication exponent, with a value of roughly $2.37$ in theory, and up to $3$ in practice). For the case of random SVM (support vector machine) instances of size $O(n)$, the quantum algorithm scales as $O(n^k)$, where the exponent $k$ is estimated to be $2.59$ using a least-squares power law. On the same family random instances, the estimated scaling exponent for an external SOCP solver is $3.31$ while that for a state-of-the-art SVM solver is $3.11$.
翻译:我们为二阶锥形编程(SOCP)提出了一个量子内点法(IPM) 美元, 该值在时间上运行 $\ zeta$, 该值由美元=sqrt{O} 美元=左( n\ sqrt{r}\ frac_zeta\ kapa\ kapa\ kdelta2}\ log\ left(1/\\ epsilon\right)\right) 美元, 其中美元是SOCP的等级和维度, 其中美元是美元=xxxxxxl( 美元=xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx