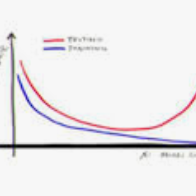
This work studies the generalization error of gradient methods. More specifically, we focus on how training steps $T$ and step-size $\eta$ might affect generalization in smooth stochastic convex optimization (SCO) problems. We first provide tight excess risk lower bounds for Gradient Descent (GD) and Stochastic Gradient Descent (SGD) under the general non-realizable smooth SCO setting, suggesting that existing stability analyses are tight in step-size and iteration dependence, and that overfitting provably happens. Next, we study the case when the loss is realizable, i.e. an optimal solution minimizes all the data points. Recent works show better rates can be attained but the improvement is reduced when training time is long. Our paper examines this observation by providing excess risk lower bounds for GD and SGD in two realizable settings: 1) $\eta T = \bigO{n}$, and (2) $\eta T = \bigOmega{n}$, where $n$ is the size of dataset. In the first case $\eta T = \bigOmega{n}$, our lower bounds tightly match and certify the respective upper bounds. However, for the case $\eta T = \bigOmega{n}$, our analysis indicates a gap between the lower and upper bounds. A conjecture is proposed that the gap can be closed by improving upper bounds, supported by analyses in two special scenarios.
翻译:暂无翻译