Statistical and Computational Trade-offs in Variational Inference: A Case Study in Inferential Model Selection

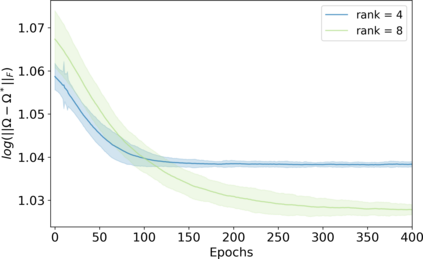
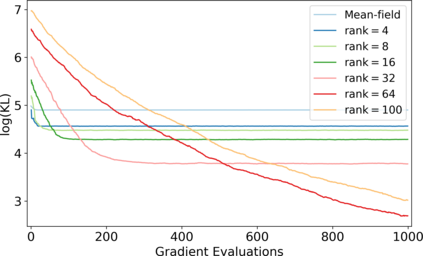
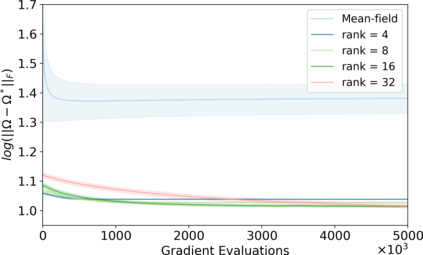
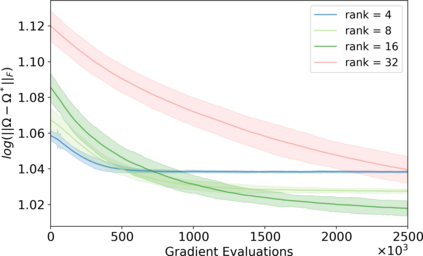
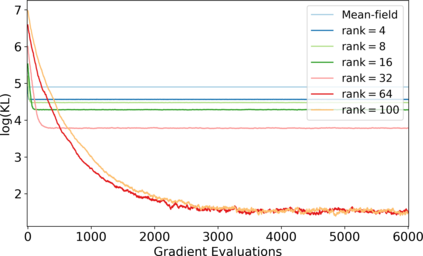
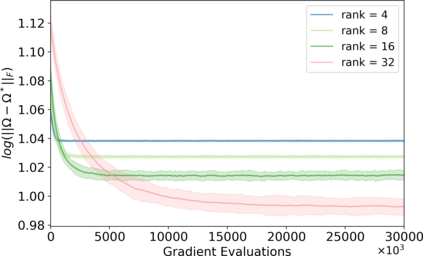
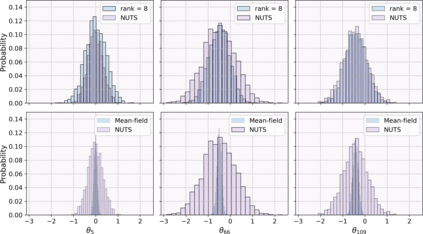
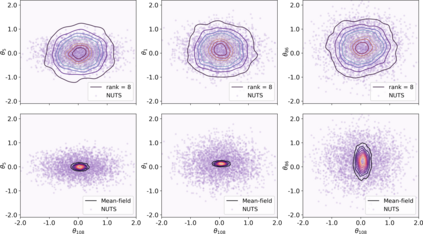
Variational inference has recently emerged as a popular alternative to the classical Markov chain Monte Carlo (MCMC) in large-scale Bayesian inference. The core idea of variational inference is to trade statistical accuracy for computational efficiency. It aims to approximate the posterior, reducing computation costs but potentially compromising its statistical accuracy. In this work, we study this statistical and computational trade-off in variational inference via a case study in inferential model selection. Focusing on Gaussian inferential models (a.k.a. variational approximating families) with diagonal plus low-rank precision matrices, we initiate a theoretical study of the trade-offs in two aspects, Bayesian posterior inference error and frequentist uncertainty quantification error. From the Bayesian posterior inference perspective, we characterize the error of the variational posterior relative to the exact posterior. We prove that, given a fixed computation budget, a lower-rank inferential model produces variational posteriors with a higher statistical approximation error, but a lower computational error; it reduces variances in stochastic optimization and, in turn, accelerates convergence. From the frequentist uncertainty quantification perspective, we consider the precision matrix of the variational posterior as an uncertainty estimate. We find that, relative to the true asymptotic precision, the variational approximation suffers from an additional statistical error originating from the sampling uncertainty of the data. Moreover, this statistical error becomes the dominant factor as the computation budget increases. As a consequence, for small datasets, the inferential model need not be full-rank to achieve optimal estimation error. We finally demonstrate these statistical and computational trade-offs inference across empirical studies, corroborating the theoretical findings.