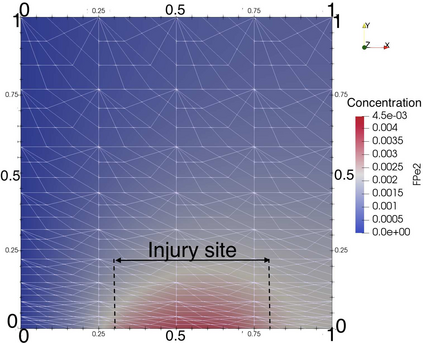
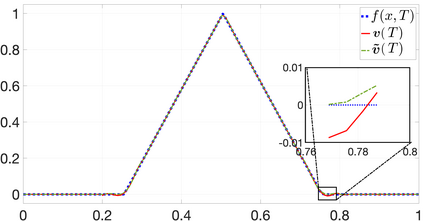
Finite element simulations have been used to solve various partial differential equations (PDEs) that model physical, chemical, and biological phenomena. The resulting discretized solutions to PDEs often do not satisfy requisite physical properties, such as positivity or monotonicity. Such invalid solutions pose both modeling challenges, since the physical interpretation of simulation results is not possible, and computational challenges, since such properties may be required to advance the scheme. We, therefore, consider the problem of computing solutions that preserve these structural solution properties, which we enforce as additional constraints on the solution. We consider in particular the class of convex constraints, which includes positivity and monotonicity. By embedding such constraints as a postprocessing convex optimization procedure, we can compute solutions that satisfy general types of convex constraints. For certain types of constraints (including positivity and monotonicity), the optimization is a filter, i.e., a norm-decreasing operation. We provide a variety of tests on one-dimensional time-dependent PDEs that demonstrate the method's efficacy, and we empirically show that rates of convergence are unaffected by the inclusion of the constraints.
翻译:因此,我们考虑了计算机解决方案的问题,这些解决方案维护了这些结构性解决方案的特性,这是我们对解决方案的额外限制。我们特别考虑了包括假设性和单一性在内的二次曲线制约的类别。通过嵌入后处理的二次曲线优化程序等制约,我们可以计算出满足一般类型的二次曲线制约的解决方案。对于某些类型的制约(包括假设性和单一性),优化是一种过滤器,即规范-消化操作。我们提供了各种基于一维时间的测试,以显示方法的功效,我们从实验角度表明趋同速度不受影响。
相关内容
Source: Apple - iOS 8