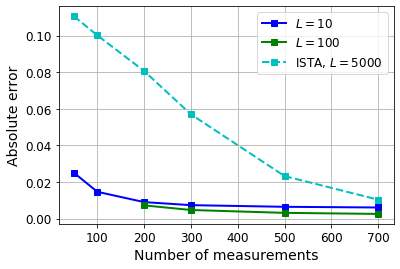
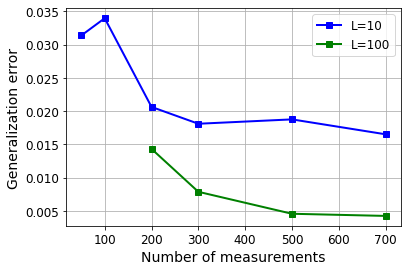
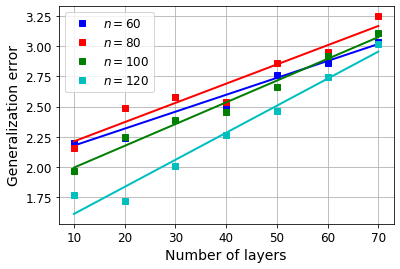
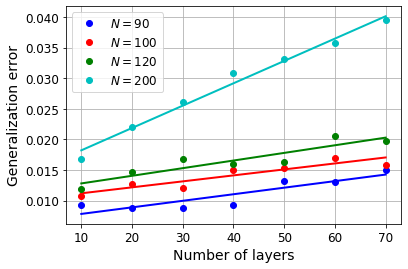
Various iterative reconstruction algorithms for inverse problems can be unfolded as neural networks. Empirically, this approach has often led to improved results, but theoretical guarantees are still scarce. While some progress on generalization properties of neural networks have been made, great challenges remain. In this chapter, we discuss and combine these topics to present a generalization error analysis for a class of neural networks suitable for sparse reconstruction from few linear measurements. The hypothesis class considered is inspired by the classical iterative soft-thresholding algorithm (ISTA). The neural networks in this class are obtained by unfolding iterations of ISTA and learning some of the weights. Based on training samples, we aim at learning the optimal network parameters via empirical risk minimization and thereby the optimal network that reconstructs signals from their compressive linear measurements. In particular, we may learn a sparsity basis that is shared by all of the iterations/layers and thereby obtain a new approach for dictionary learning. For this class of networks, we present a generalization bound, which is based on bounding the Rademacher complexity of hypothesis classes consisting of such deep networks via Dudley's integral. Remarkably, under realistic conditions, the generalization error scales only logarithmically in the number of layers, and at most linear in number of measurements.
翻译:针对反面问题的各种迭代重建算法可以作为神经网络展开。 典型的迭代软保存算法( ISTA) 启发了人们的假设类。 这一类的神经网络是通过不断演化ISTA的迭代和学习一些重量来获得的。 根据培训样本,我们的目标是通过实验风险最小化来学习最佳网络参数,从而通过实验风险最小化和最佳网络重建信号的最佳网络。在本章中,我们讨论并结合这些专题,为适合稀有重建的一类神经网络提供概括性错误分析,从少量线性测量中得出。特别是,我们可能从所有线性/层中学习一个宽度基础,从而获得一种新的字典学习方法。 对于这一类的假设类,我们提出一个概括性约束,其基础是将Rademacher的假设类的复杂性绑在一起,这些深度网络在现实的、最精确的、最精确的层次的线性测量中,仅根据现实的、最精确的、最精确的层次的线性层次上。