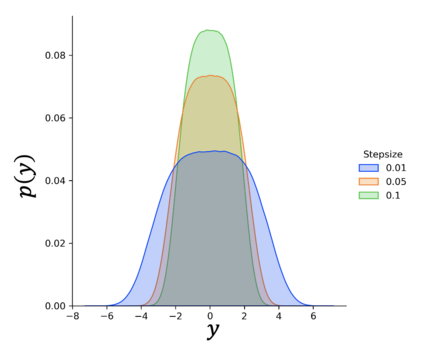
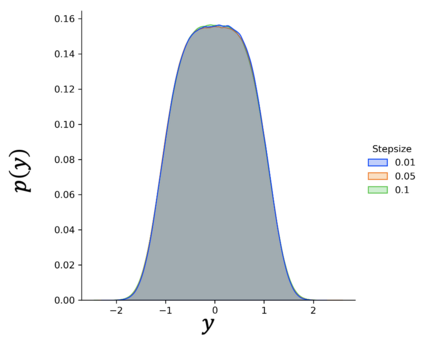
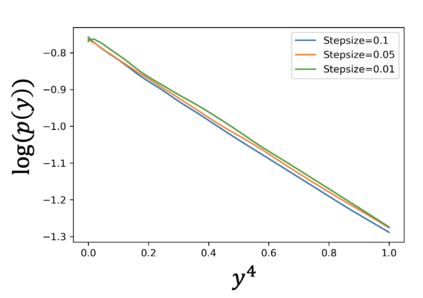
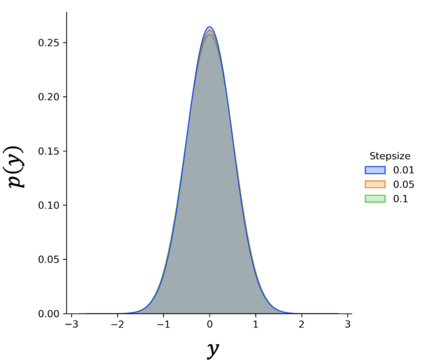
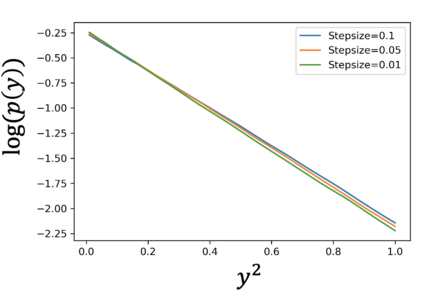
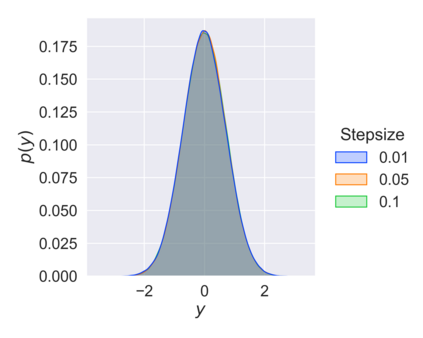
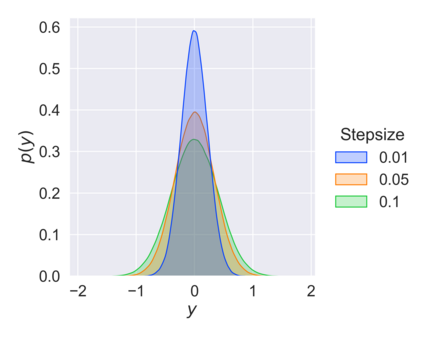
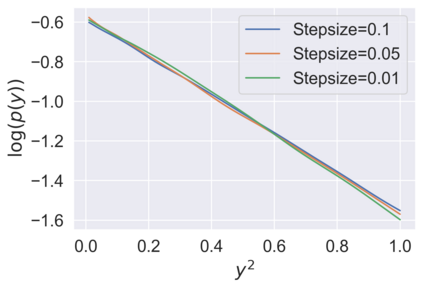
Stochastic approximation (SA) and stochastic gradient descent (SGD) algorithms are work-horses for modern machine learning algorithms. Their constant stepsize variants are preferred in practice due to fast convergence behavior. However, constant step stochastic iterative algorithms do not converge asymptotically to the optimal solution, but instead have a stationary distribution, which in general cannot be analytically characterized. In this work, we study the asymptotic behavior of the appropriately scaled stationary distribution, in the limit when the constant stepsize goes to zero. Specifically, we consider the following three settings: (1) SGD algorithms with smooth and strongly convex objective, (2) linear SA algorithms involving a Hurwitz matrix, and (3) nonlinear SA algorithms involving a contractive operator. When the iterate is scaled by $1/\sqrt{\alpha}$, where $\alpha$ is the constant stepsize, we show that the limiting scaled stationary distribution is a solution of an integral equation. Under a uniqueness assumption (which can be removed in certain settings) on this equation, we further characterize the limiting distribution as a Gaussian distribution whose covariance matrix is the unique solution of a suitable Lyapunov equation. For SA algorithms beyond these cases, our numerical experiments suggest that unlike central limit theorem type results: (1) the scaling factor need not be $1/\sqrt{\alpha}$, and (2) the limiting distribution need not be Gaussian. Based on the numerical study, we come up with a formula to determine the right scaling factor, and make insightful connection to the Euler-Maruyama discretization scheme for approximating stochastic differential equations.
翻译:软缩近似(SA) 和 斜坡下游(SGD) 算法是现代机器学习算法的工马。 由于快速趋同行为, 他们实际上偏好不断的阶梯变异。 然而, 恒定的阶梯迭代算法不会在无休止的情况下与最佳解决方案趋同, 而是有一个固定的分布, 一般来说无法进行分析。 在这项工作中, 我们研究适当缩放的固定分布的不稳行为, 在恒定步骤变为零时的极限。 具体地说, 我们考虑以下三个设置:(1) 具有平滑和强烈的螺旋目标的 SGD 算法, (2) 涉及Hurwitz 矩阵的线性 SA 运算法, 以及(3) 非线性 SA 迭代算法运算法, 以1/\qrt; $\ alphapha 平面值表示, 缩放缩缩缩缩放的固定分布法, 而不是以缩放法计算。