How is Time Frequency Space Modulation Related to Short Time Fourier Signaling?

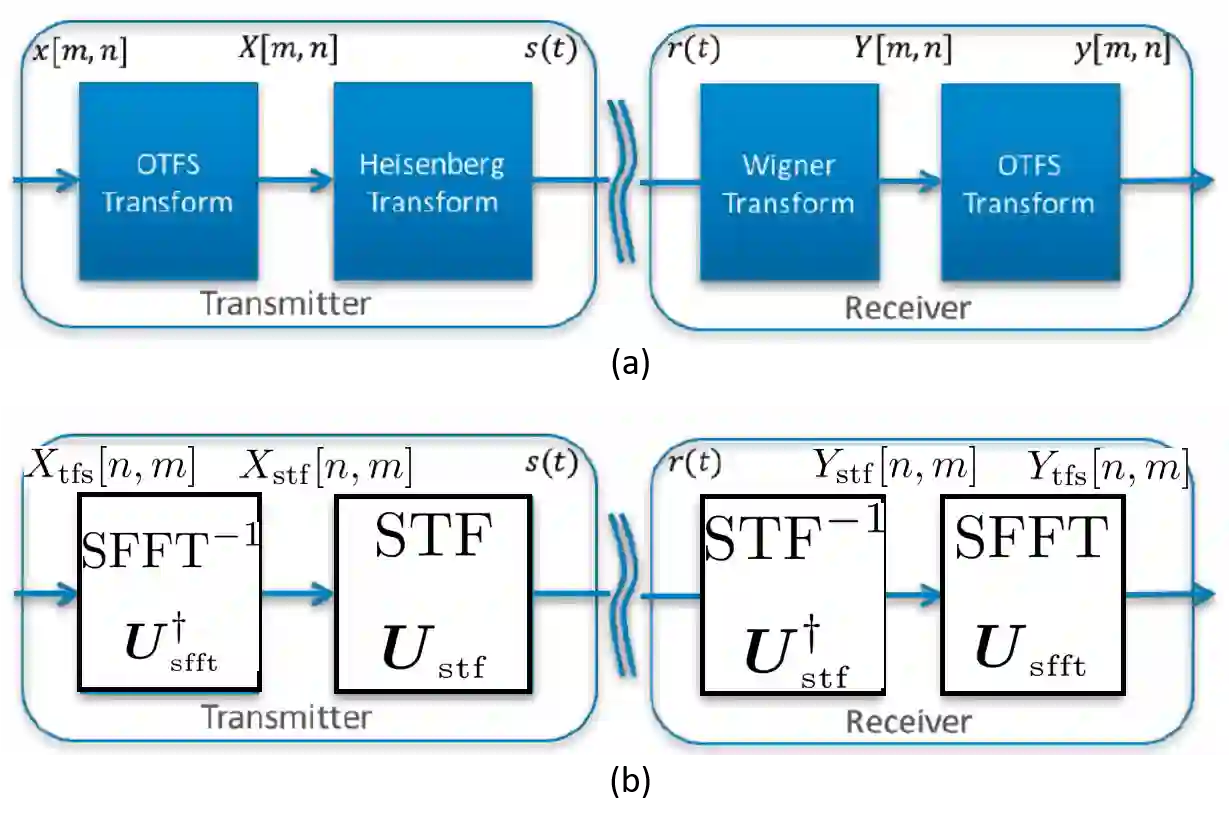
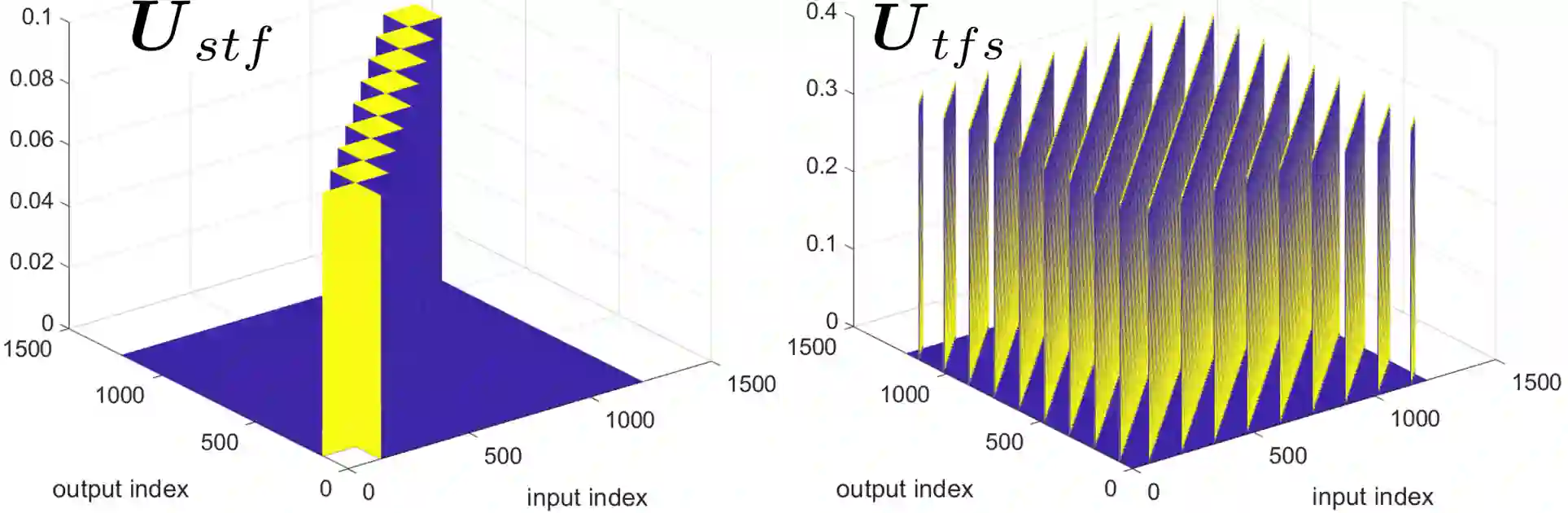
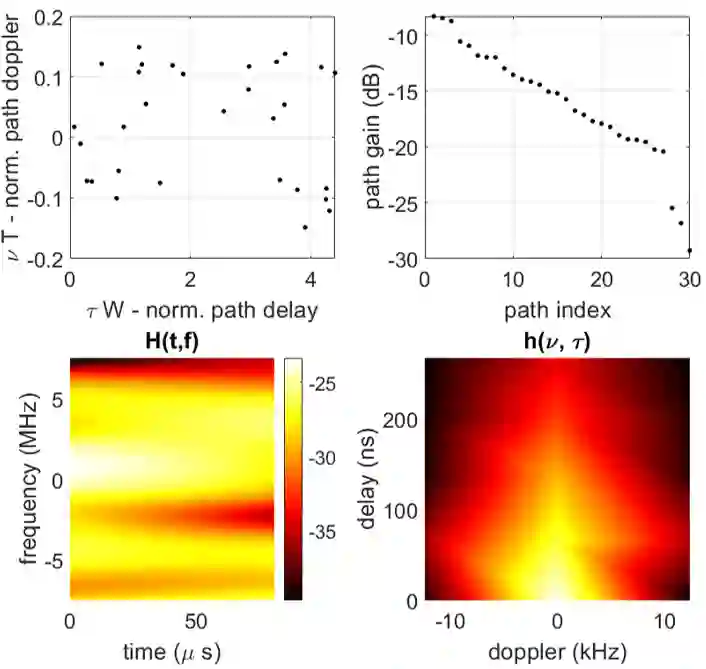
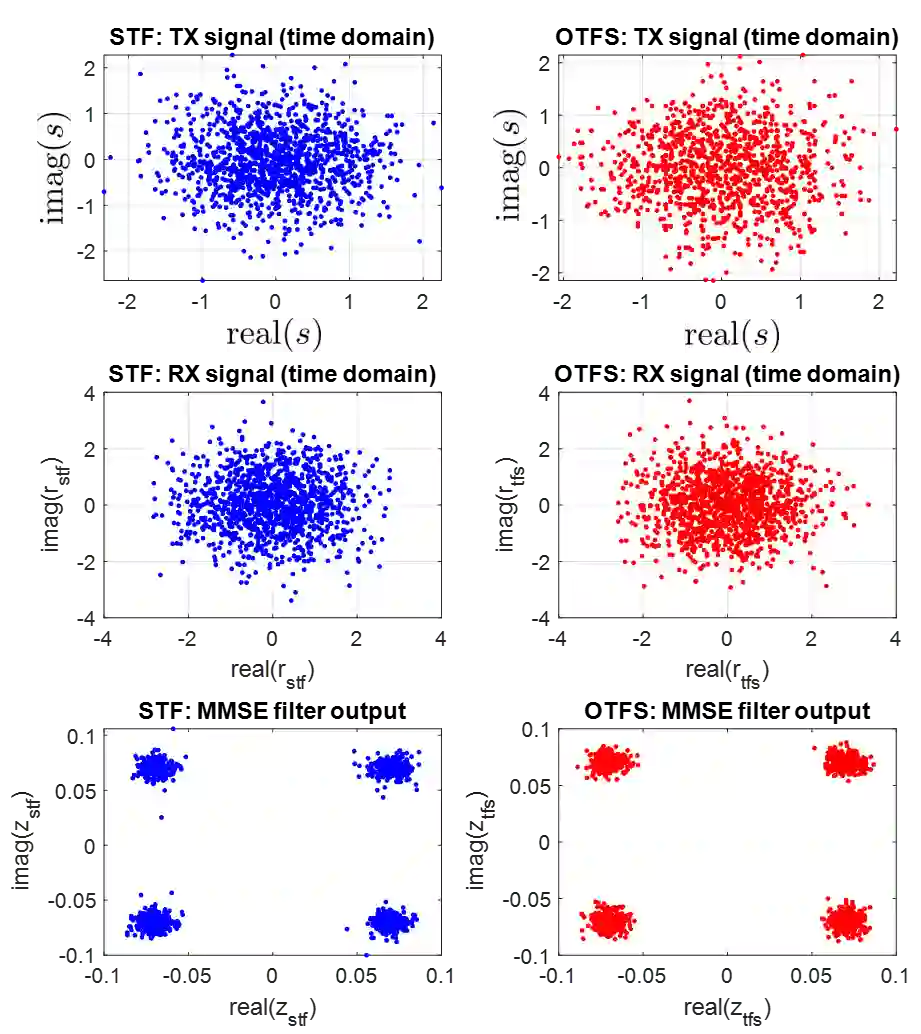
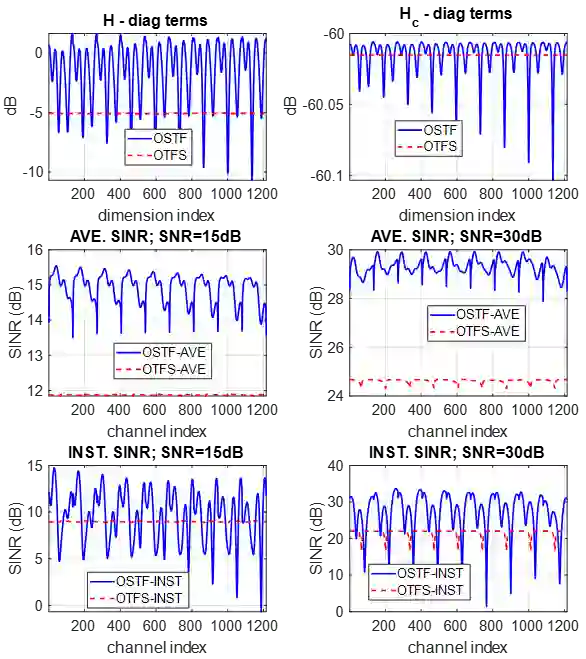
We investigate the relationship between Orthogonal Time Frequency Space (OTFS) modulation and Orthogonal Short Time Fourier (OSTF) signaling. OTFS was recently proposed as a new scheme for high Doppler scenarios and builds on OSTF. We first show that the two schemes are unitarily equivalent in the digital domain. However, OSTF defines the analog-digital interface with the waveform domain. We then develop a critically sampled matrix-vector model for the two systems and consider linear minimum mean-squared error (MMSE) filtering at the receiver to suppress inter-symbol interference. Initial comparison of capacity and (uncoded) probability of error reveals a surprising observation: OTFS under-performs OSTF in capacity but over-performs in probability of error. This result can be attributed to characteristics of the channel matrices induced by the two systems. In particular, the diagonal entries of OTFS matrix exhibit nearly identical magnitude, whereas those of the OSTF matrix exhibit wild fluctuations induced by multipath randomness. It is observed that by simply replacing the unitary matrix, relating OTFS to OSTF, by an arbitrary unitary matrix results in performance nearly identical to OTFS. We then extend our analysis to orthogonal frequency division multiplexing (OFDM) and also consider a more extreme scenario of relatively large delay and Doppler spreads. Our results demonstrate the significance of using OSTF basis waveforms rather than sinusoidal ones in OFDM in highly dynamic environments, and also highlight the impact of the level of channel state information used at the receiver.