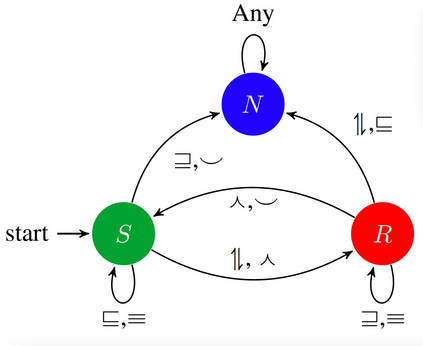
We propose ProoFVer, a proof system for fact verification using natural logic. The textual entailment model in ProoFVer is a seq2seq model generating valid natural-logic based logical inferences as its proofs. The generation of proofs makes ProoFVer an explainable system. The proof consists of iterative lexical mutations of spans in the claim with spans in a set of retrieved evidence sentences. Further, each such mutation is marked with an entailment relation using natural logic operators. The veracity of a claim is determined solely based on the sequence of natural logic relations present in the proof. By design, this makes ProoFVer a faithful by construction system that generates faithful explanations. ProoFVer outperforms existing fact-verification models, with more than two percent absolute improvements in performance and robustness. In addition to its explanations being faithful, ProoFVer also scores high on rationale extraction, with a five point absolute improvement compared to attention-based rationales in existing models. Finally, we find that humans correctly simulate ProoFVer's decisions more often using the proofs, than the decisions of an existing model that directly use the retrieved evidence for decision making.
翻译:我们提出使用自然逻辑进行事实核查的证明系统ProoFVer 。 ProoFVer 中的文本包含模型是产生有效自然逻辑逻辑推断的后继2seq 模型。 产生证明使ProoFVer 成为一个可以解释的系统。 证据包括索赔中带有一系列检索证据句中跨度的重复性法变异。 此外, 每种变异都以自然逻辑操作者为诱因关系标志。 索赔的真实性完全根据证据中存在的自然逻辑关系序列来确定。 设计上, ProoFVer 使ProoFVer 成为建筑系统的忠实信徒, 产生忠实的解释。 ProoFVer 超越了现有的事实验证模型, 其性能和稳健性方面有超过2%的绝对改进。 除了解释外, ProoFVer 还在理由提取方面得分高, 与现有模型中基于关注的理由相比, 5点绝对性改进。 最后, 我们发现, 人类正确模拟ProoFVer 的决定, 更经常使用现有的证据, 而不是直接使用现有决定。