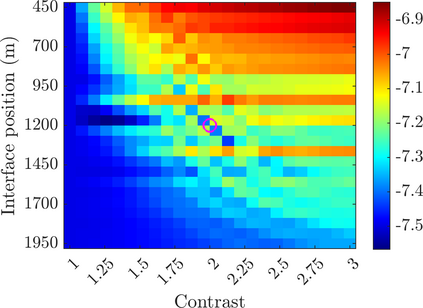
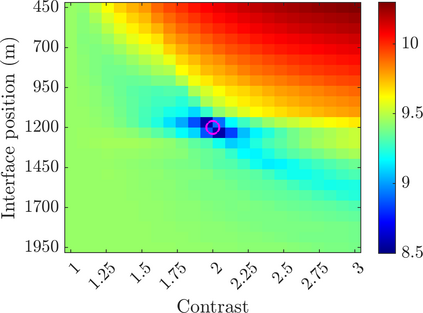
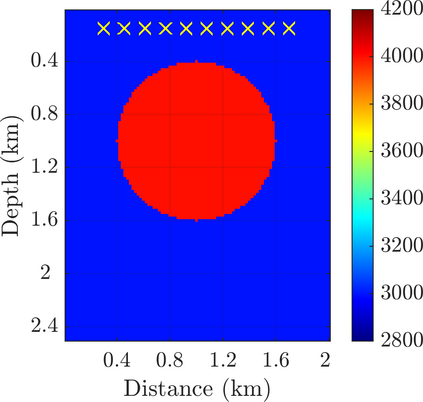
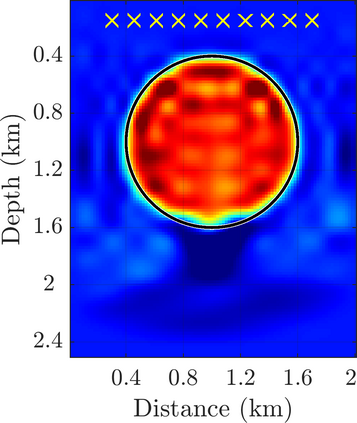
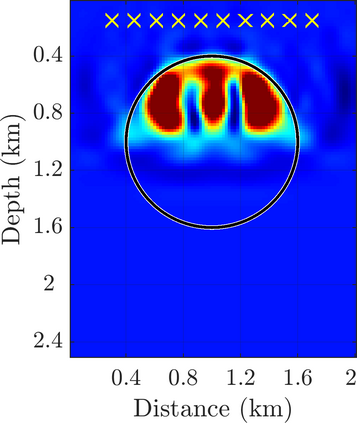
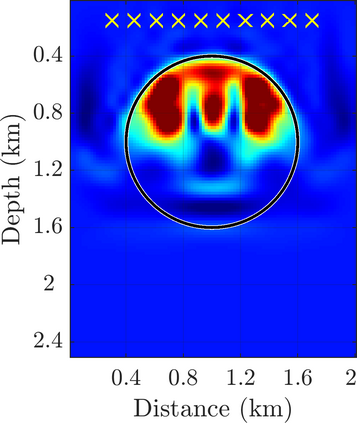
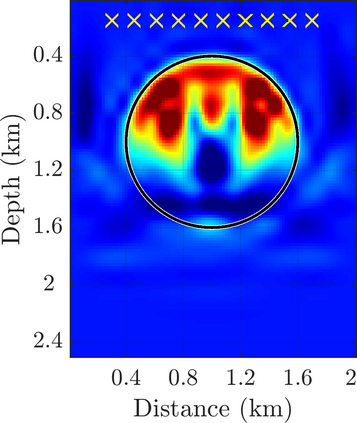
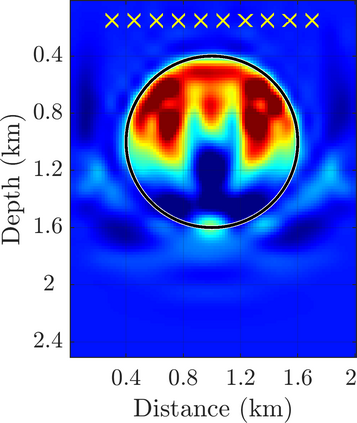
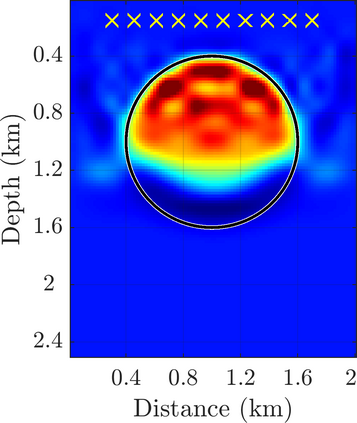
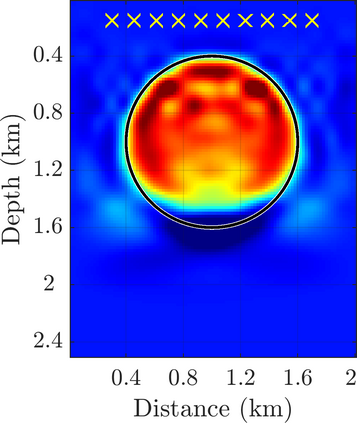
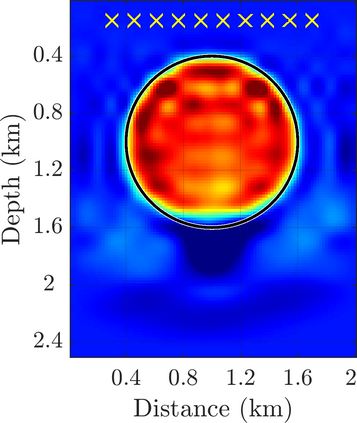
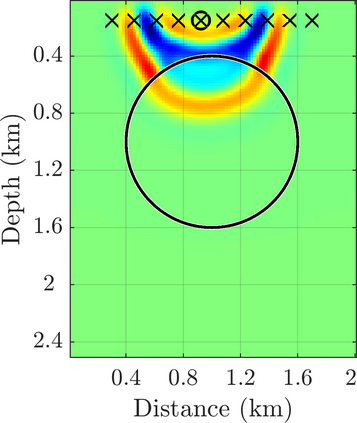
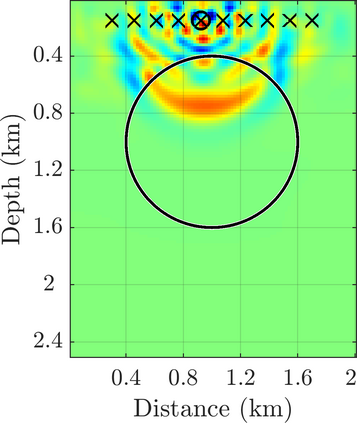
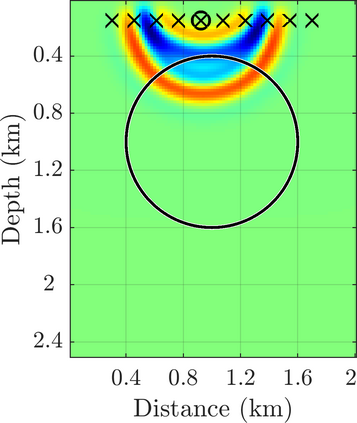
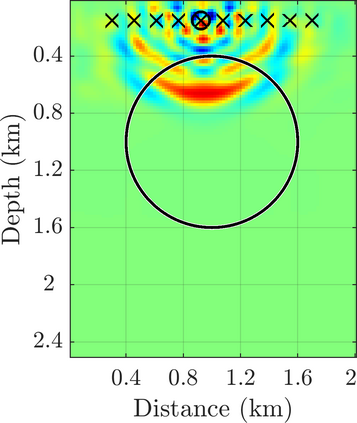
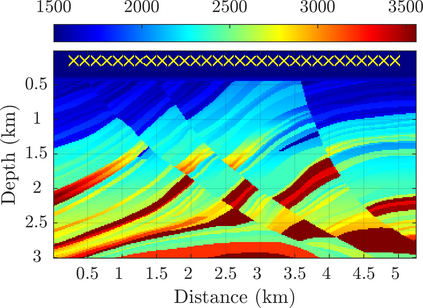
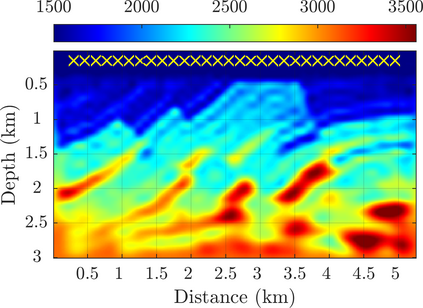
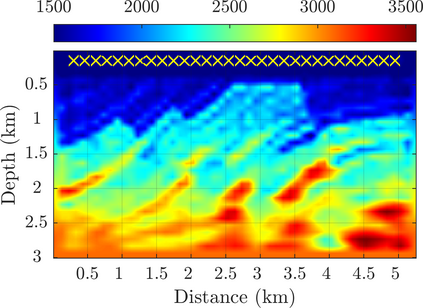
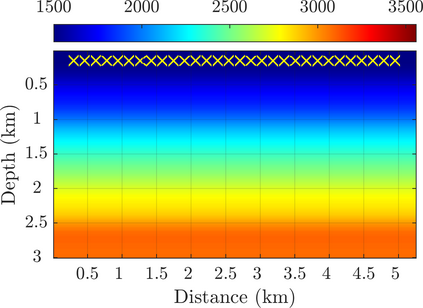
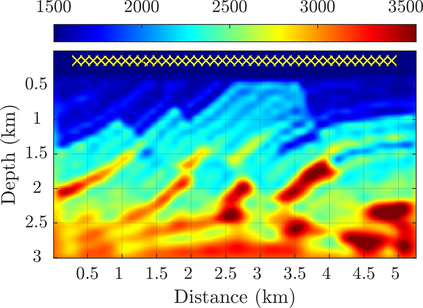
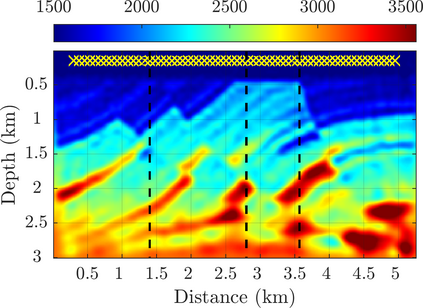
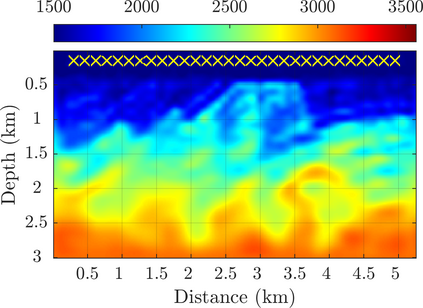
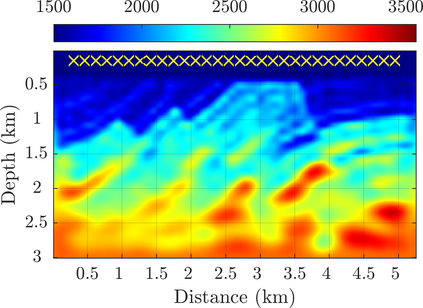
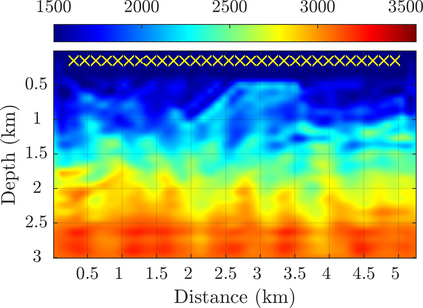
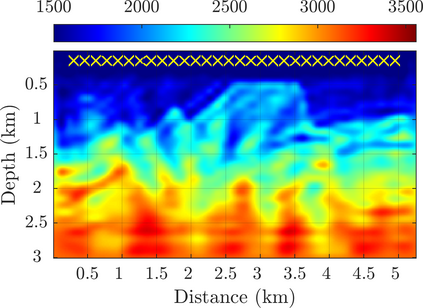
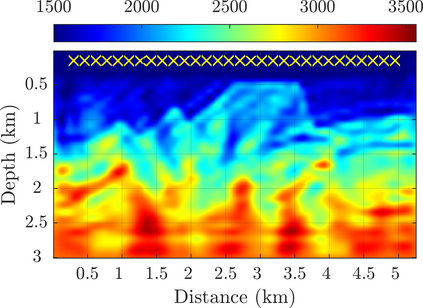
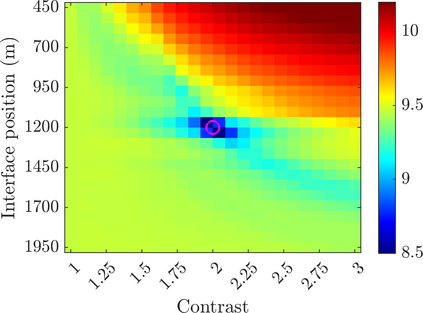
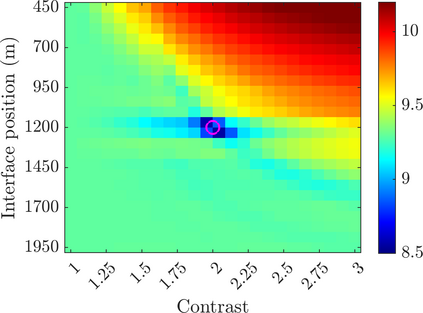
We introduce a novel approach to waveform inversion, based on a data driven reduced order model (ROM) of the wave operator. The presentation is for the acoustic wave equation, but the approach can be extended to elastic or electromagnetic waves. The data are time resolved measurements of the pressure wave at the sensors in an active array, which probe the unknown medium with pulses and measure the generated waves. The ROM depends nonlinearly on the data but it can be constructed from them using numerical linear algebra methods. We show that the ROM can be used for the inverse problem of velocity estimation. While the full-waveform inversion approach of {nonlinear least-squares} data fitting is challenging without low frequency information, due to multiple minima of the objective function, the minimization of the ROM misfit function has a better behavior, even for a poor initial guess. In fact, the ROM misfit function is demonstrably a convex function for low-dimensional parametrizations of the unknown velocity. We give the construction of the ROM, introduce the inversion approach based on the ROM misfit and assess its performance with numerical simulations.
翻译:我们引入了一种基于数据驱动的波形倒转模型(ROM)的波形转换新方法。 演示是用于声波方程的, 但该方法可以扩展至弹性波或电磁波。 数据是动态阵列传感器压力波的时间分辨率测量, 该阵列用脉冲探测未知介质并测量产生的波。 该阵列非线性地依赖数据, 但可以用数字线性代数法从数据中构建。 我们显示, ROM 可用于反向速度估测问题 。 虽然 { 非线性最小平方} 数据安装全波反向方法在没有低频率信息的情况下具有挑战性, 但由于目标功能的多重迷你功能, 将ROM 的错误功能最小化具有更好的行为方式, 即使是最初的猜测不力。 事实上, ROM 的错误功能是用于低维度对未知速度的准的直线性函数。 我们给出了ROM 的构造, 引入基于 ROM 错误的反向方法, 并用模拟的数字评估其性能 。