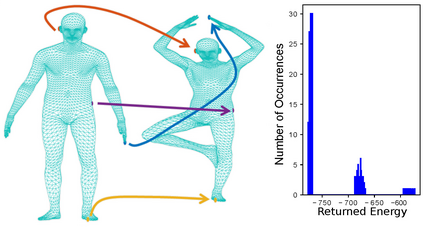
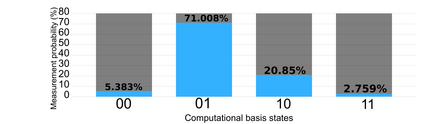
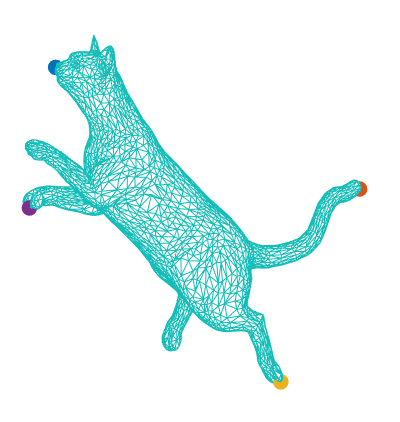
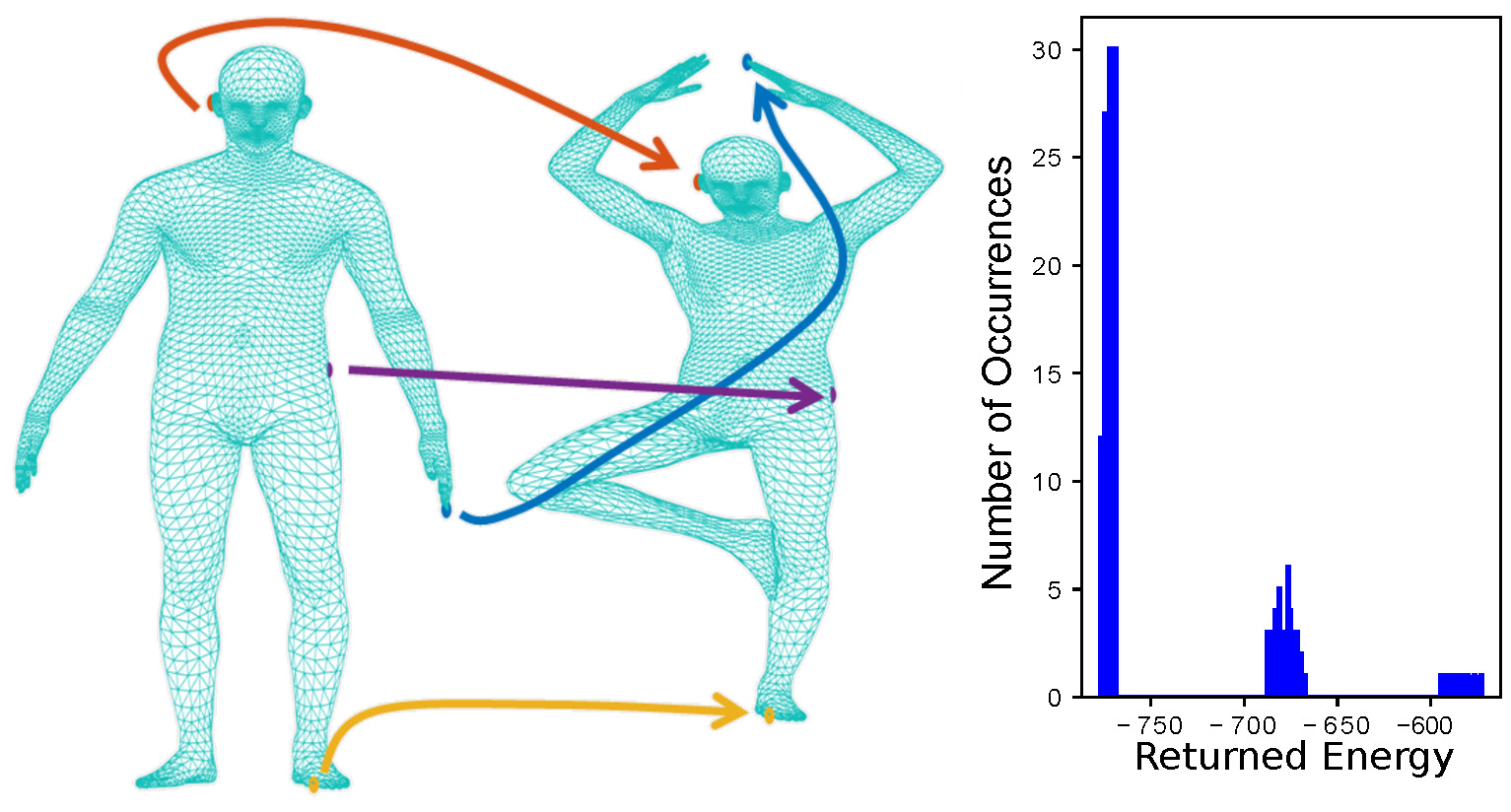
Matching problems on 3D shapes and images are challenging as they are frequently formulated as combinatorial quadratic assignment problems (QAPs) with permutation matrix constraints, which are NP-hard. In this work, we address such problems with emerging quantum computing technology and propose several reformulations of QAPs as unconstrained problems suitable for efficient execution on quantum hardware. We investigate several ways to inject permutation matrix constraints in a quadratic unconstrained binary optimization problem which can be mapped to quantum hardware. We focus on obtaining a sufficient spectral gap, which further increases the probability to measure optimal solutions and valid permutation matrices in a single run. We perform our experiments on the quantum computer D-Wave 2000Q (2^11 qubits, adiabatic). Despite the observed discrepancy between simulated adiabatic quantum computing and execution on real quantum hardware, our reformulation of permutation matrix constraints increases the robustness of the numerical computations over other penalty approaches in our experiments. The proposed algorithm has the potential to scale to higher dimensions on future quantum computing architectures, which opens up multiple new directions for solving matching problems in 3D computer vision and graphics.
翻译:3D 形状和图像的匹配问题具有挑战性,因为这些问题往往是作为组合四级分配问题(QAPs)而形成的,具有调异矩阵限制,是NP-硬性。在这项工作中,我们用新兴量子计算技术解决这类问题,并提议对QAP进行若干次重新配方,作为适合量子硬件高效执行的不受限制的问题。我们调查了几种方法,在可被映射为量子硬件的四级未受限制的二进制优化问题中注入变异矩阵限制。我们侧重于获得足够的光谱差距,从而进一步增加在单一运行中测量最佳解决方案和有效调异矩阵的可能性。我们在量子计算机D-Wave 2000Q (2 ⁇ 11 qubits, adiabatic) 上进行量子计算机量子计算机量子计算机量子计算机模拟计算与实际量子硬件执行之间观察到的差异,但我们的变异体矩阵限制增加了数值计算比量子硬件其他罚款方法的强度。我们提出的算法有可能将未来量子计算机计算结构的更高尺寸,这为3D 图形和图像的匹配问题打开了多个新方向。