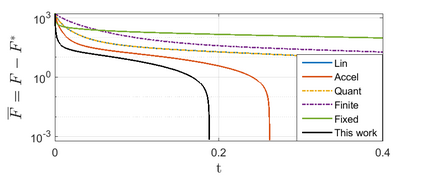
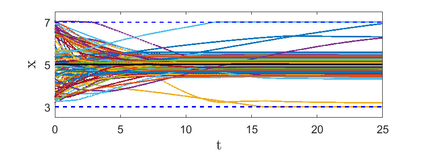
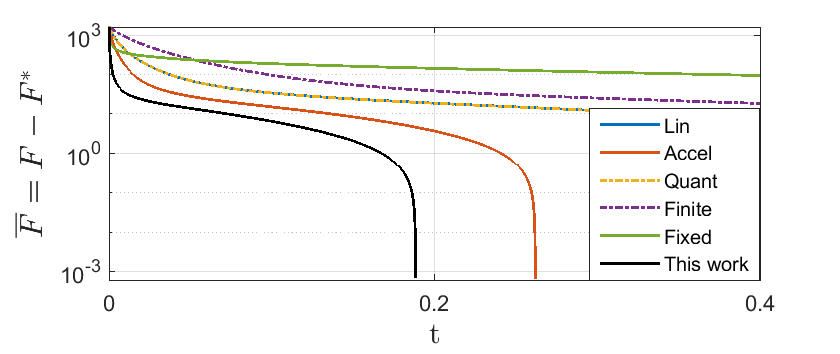
This paper proposes networked dynamics to solve resource allocation problems over time-varying multi-agent networks. The state of each agent represents the amount of used resources (or produced utilities) while the total amount of resources is fixed. The idea is to optimally allocate the resources among the group of agents by minimizing the overall cost function subject to fixed sum of resources. Each agents' information is restricted to its own state and cost function and those of its immediate in-neighbors. This is motivated by distributed applications such as mobile edge-computing, economic dispatch over smart grids, and multi-agent coverage control. This work provides a fast convergent solution (in comparison with linear dynamics) while considering relaxed network connectivity with quantized communication links. The proposed dynamics reaches optimal solution over switching (possibly disconnected) undirected networks as far as their union over some bounded non-overlapping time-intervals has a spanning-tree. We prove feasibility of the solution, uniqueness of the optimal state, and convergence to the optimal value under the proposed dynamics, where the analysis is applicable to similar 1st-order allocation dynamics with strongly sign-preserving nonlinearities, such as actuator saturation.
翻译:本文提出了解决时间变化多试剂网络资源分配问题的网络动态。每个代理商的状况代表了使用的资源(或生产的公用事业)的数量,而资源总量是固定的。想法是最大限度地减少资源固定总和下的总体成本功能,从而在代理商群体中优化资源的分配。每个代理商的信息仅限于其自身的状态和成本功能,以及其直接邻接的状态和成本功能。这得益于移动边缘计算、智能网格上的经济发送和多试剂覆盖控制等分布式应用程序。这项工作提供了快速集中的解决方案(与线性动态相比),同时考虑与量化通信链接的网络连接性放松。拟议的动态在转换(可能断开的)无定向网络方面达到了最佳解决方案,只要它们结合某些封闭的不重叠时间互动网络就具有覆盖性。我们证明了解决方案的可行性、最佳状态的独特性以及与拟议动态下的最佳价值的趋同性,其中的分析适用于类似的第1级分配动态,同时保持强烈的信号非饱和性,例如动作。