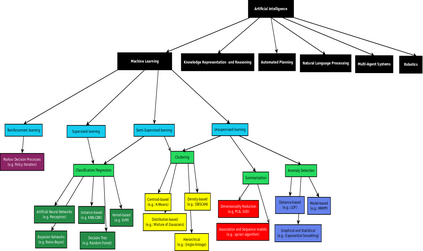
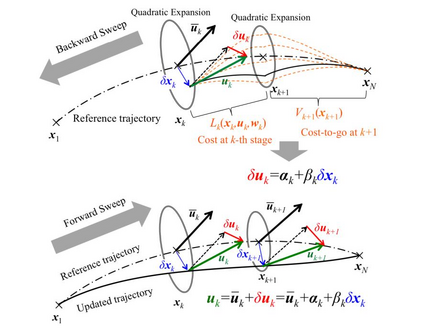
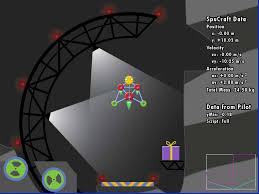
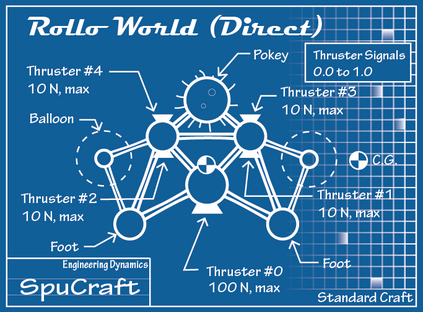
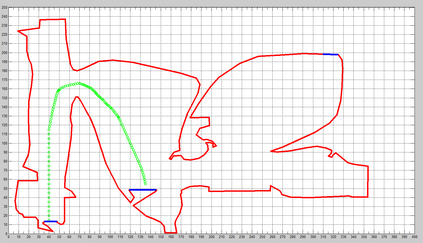
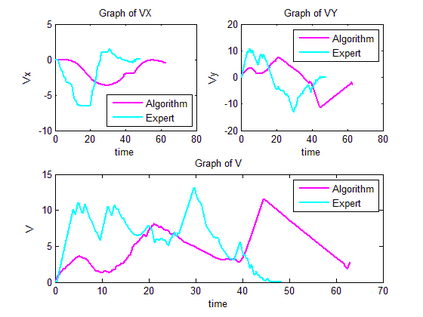
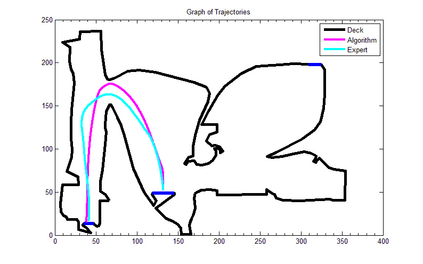
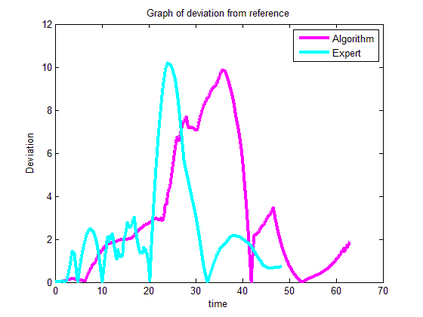
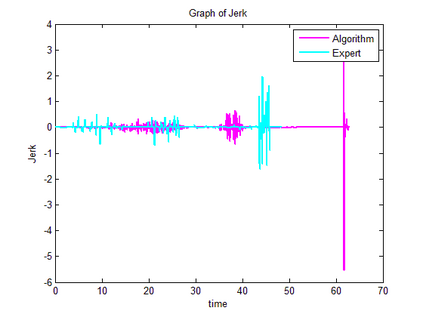
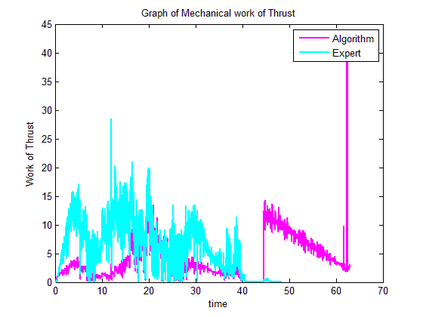
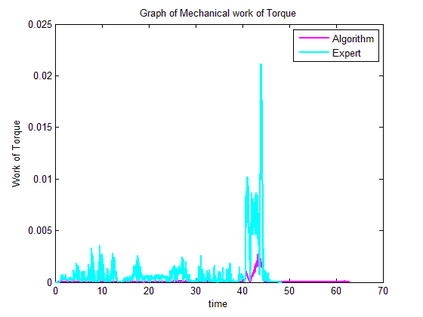
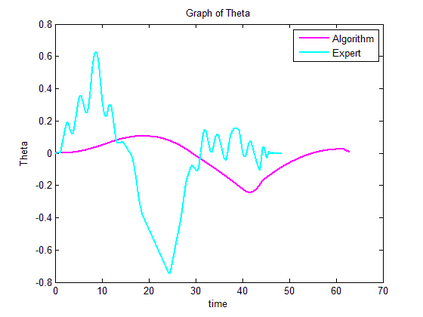
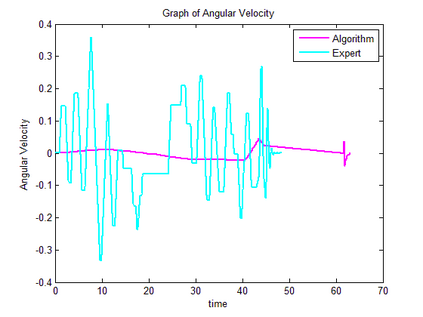
Trajectory following is one of the complicated control problems when its dynamics are nonlinear, stochastic and include a large number of parameters. The problem has significant difficulties including a large number of trials required for data collection and a massive volume of computations required to find a closed-loop controller for high dimensional and stochastic domains. For solving this type of problem, if we have an appropriate reward function and dynamics model; finding an optimal control policy is possible by using model-based reinforcement learning and optimal control algorithms. However, defining an accurate dynamics model is not possible for complicated problems. Pieter Abbeel and Andrew Ng recently presented an algorithm that requires only an approximate model and only a small number of real-life trials. This algorithm has broad applicability; however, there are some problems regarding the convergence of the algorithm. In this research, required modifications are presented that provide more powerful assurance for converging to optimal control policy. Also updated algorithm is implemented to evaluate the efficiency of the new algorithm by comparing the acquired results with human expert performance. We are using differential dynamic programming (DDP) as the locally trajectory optimizer, and a 2D dynamics and kinematics simulator is used to evaluate the accuracy of the presented algorithm.
翻译:当动态是非线性、随机性和包含大量参数时,轨迹跟踪是复杂的控制问题之一。问题存在重大困难,包括数据收集需要大量试验和为高维和随机性域寻找闭路控制器所需的大量计算。如果我们有适当的奖赏功能和动态模型,为了解决这类问题,有可能通过使用基于模型的强化学习和最佳控制算法找到最佳控制政策。然而,为复杂的问题确定准确的动态模型是不可能的。Pieter Abbeel和Andrew Ng最近提出了一个算法,只需要一个近似模型和少量实际生活试验。这一算法具有广泛适用性;然而,算法的趋同存在一些问题。在这项研究中,提出了必要的修改,为凝聚到最佳控制政策提供了更强有力的保证。还实施了更新的算法,通过将所获得的结果与人类专家性能进行比较来评价新算法的效率。我们正在使用差异动态编程(DDP)作为本地轨迹优化器,而2D动态和运动算法的精确度是用来评价所展示的Simator。