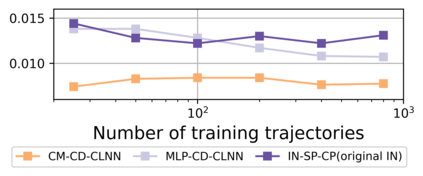
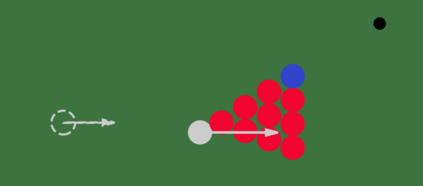
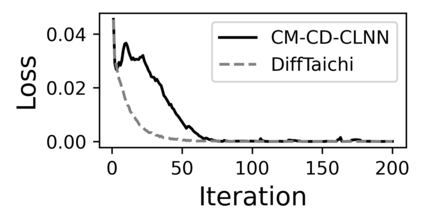
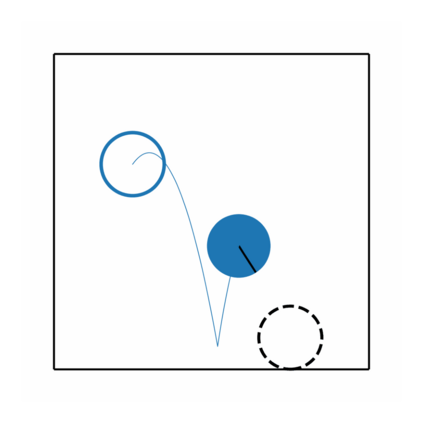
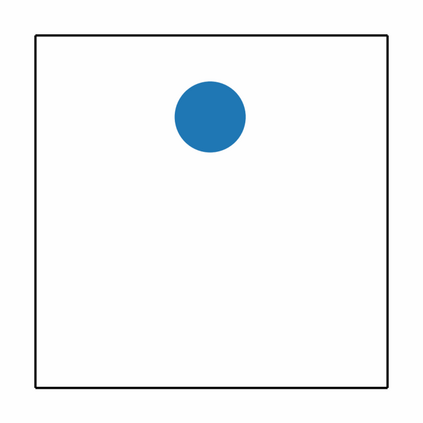
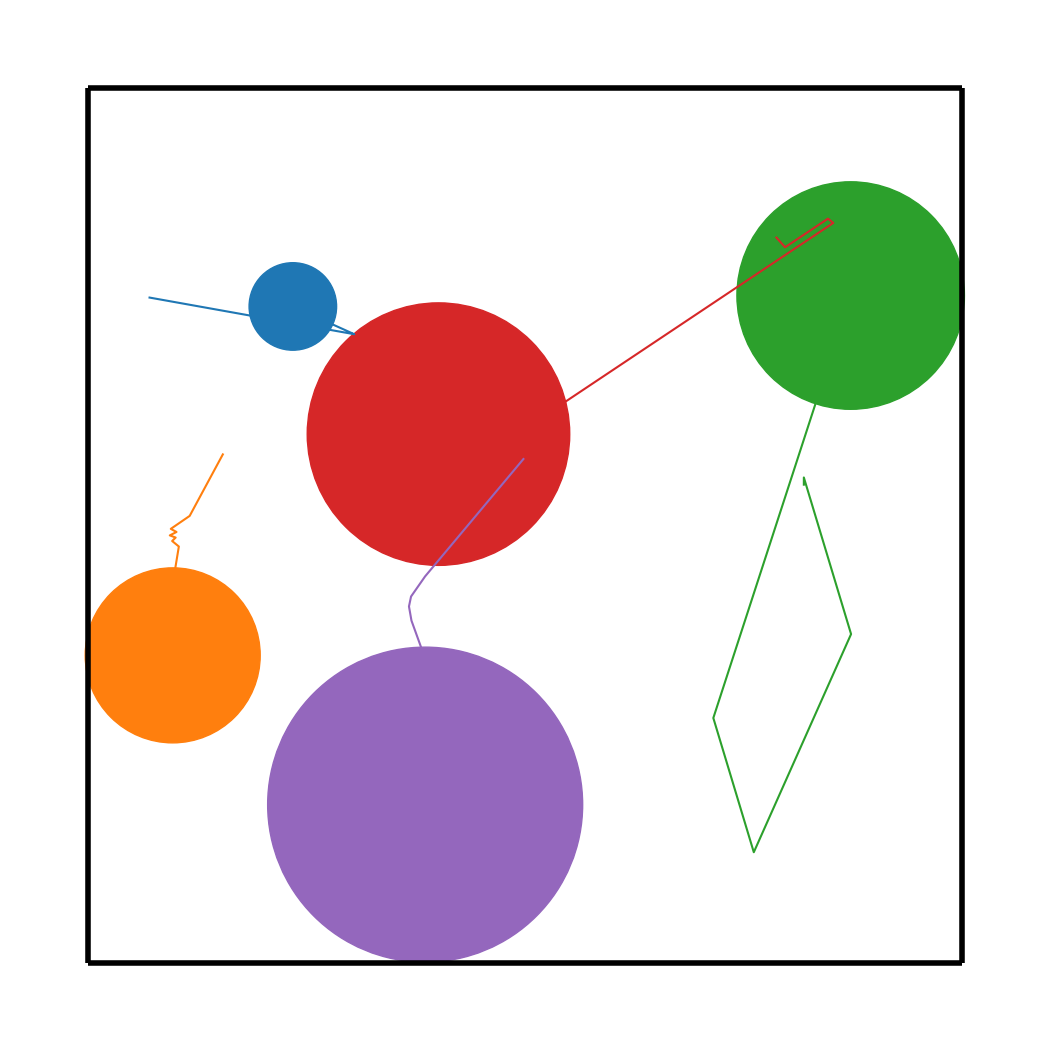
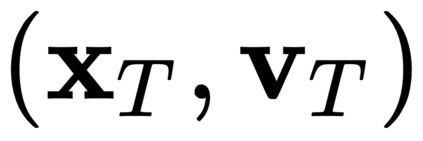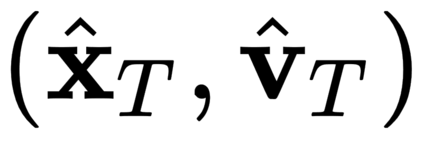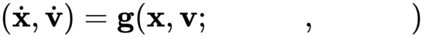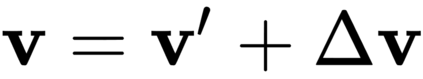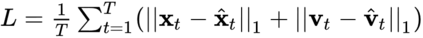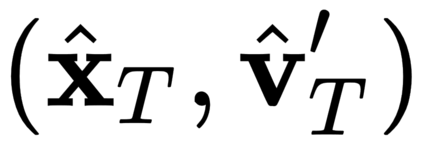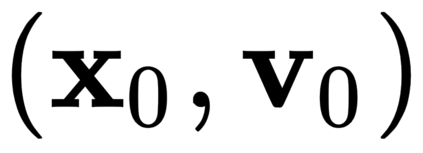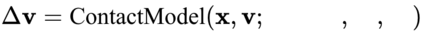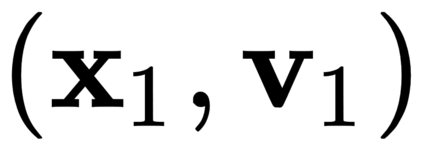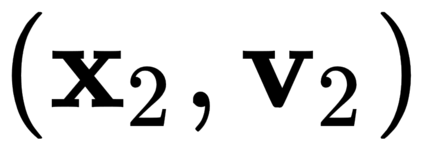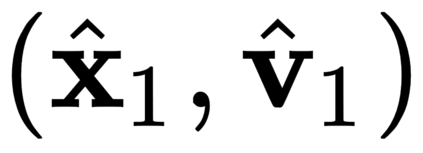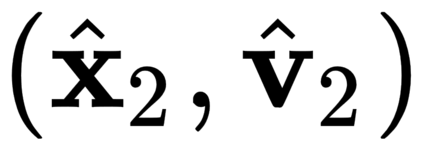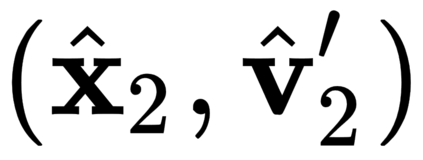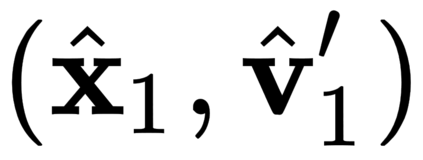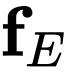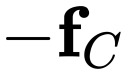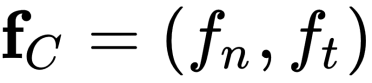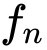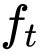The incorporation of appropriate inductive bias plays a critical role in learning dynamics from data. A growing body of work has been exploring ways to enforce energy conservation in the learned dynamics by encoding Lagrangian or Hamiltonian dynamics into the neural network architecture. These existing approaches are based on differential equations, which do not allow discontinuity in the states and thereby limit the class of systems one can learn. However, in reality, most physical systems, such as legged robots and robotic manipulators, involve contacts and collisions, which introduce discontinuities in the states. In this paper, we introduce a differentiable contact model, which can capture contact mechanics: frictionless/frictional, as well as elastic/inelastic. This model can also accommodate inequality constraints, such as limits on the joint angles. The proposed contact model extends the scope of Lagrangian and Hamiltonian neural networks by allowing simultaneous learning of contact and system properties. We demonstrate this framework on a series of challenging 2D and 3D physical systems with different coefficients of restitution and friction. The learned dynamics can be used as a differentiable physics simulator for downstream gradient-based optimization tasks, such as planning and control.
翻译:纳入适当的感官偏见在从数据中学习动态方面发挥着关键作用。越来越多的工作正在探索如何通过将拉格朗吉或汉密尔顿动态编码成神经网络结构,在所学动态中实施节能。这些现有方法基于不同方程式,不允许各州出现不连续现象,从而限制人们能够学习的系统类别。然而,在现实中,大多数物理系统,例如腿式机器人和机器人操纵器,都涉及接触和碰撞,这导致各州出现不连续现象。在本文中,我们引入了一种不同的接触模式,可以捕捉接触力:无摩/纤维,以及弹性/无线。这一模式还可以容纳不平等的制约因素,例如对联合角度的限制。拟议的接触模式扩大了拉格朗吉和汉密尔顿神经网络的范围,允许同时学习接触和系统特性。我们展示了这一框架,用于一系列具有挑战性的2D和3D物理系统,具有不同的恢复和摩擦系数。所学过的动态可以用作不同的物理模拟器,用于下游层控制,例如规划。