Scalable Bayesian inference for the generalized linear mixed model

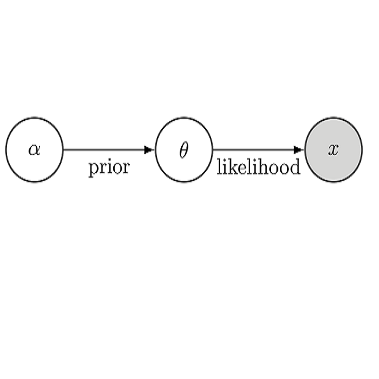
The generalized linear mixed model (GLMM) is a popular statistical approach for handling correlated data, and is used extensively in applications areas where big data is common, including biomedical data settings. The focus of this paper is scalable statistical inference for the GLMM, where we define statistical inference as: (i) estimation of population parameters, and (ii) evaluation of scientific hypotheses in the presence of uncertainty. Artificial intelligence (AI) learning algorithms excel at scalable statistical estimation, but rarely include uncertainty quantification. In contrast, Bayesian inference provides full statistical inference, since uncertainty quantification results automatically from the posterior distribution. Unfortunately, Bayesian inference algorithms, including Markov Chain Monte Carlo (MCMC), become computationally intractable in big data settings. In this paper, we introduce a statistical inference algorithm at the intersection of AI and Bayesian inference, that leverages the scalability of modern AI algorithms with guaranteed uncertainty quantification that accompanies Bayesian inference. Our algorithm is an extension of stochastic gradient MCMC with novel contributions that address the treatment of correlated data (i.e., intractable marginal likelihood) and proper posterior variance estimation. Through theoretical and empirical results we establish our algorithm's statistical inference properties, and apply the method in a large electronic health records database.