A threshold dislocation dynamics method

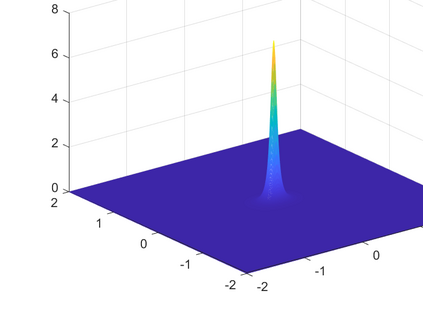
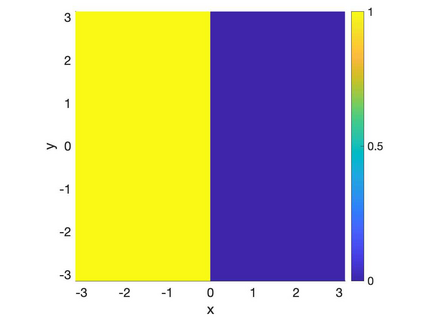
The Merriman-Bence-Osher threshold dynamics method is an efficient algorithm to simulate the motion by mean curvature, in which two steps of convolution with diffusion kernel and thresholding alternate. It has the advantages of being easy to implement and with high efficiency. In this paper, we propose an efficient threshold dynamics method for dislocation dynamics in a slip plane. We show that this proposed threshold dislocation dynamics method is able to give correct two leading orders in dislocation velocity, including both the $O(\log \varepsilon)$ local curvature force and the $O(1)$ nonlocal force due to the long-range stress field generated by the dislocations, where $\varepsilon$ is the dislocation core size. This is different from the available threshold dynamics methods in the literature which only give the leading order local velocities associated with mean curvature or its anisotropic generalizations of the moving fronts. We also propose a numerical method based on spatial variable stretching to overcome the numerical limitations brought by physical settings in this threshold dislocation dynamics method. Specifically, this variable stretching method is able to correct the mobility and to rescale the velocity, which can be applied generally to any threshold dynamics method. We validate the proposed threshold dislocation dynamics method by numerical simulations of various motions and interaction of dislocations.