Numerical methods for the mass-conserved Ohta-Kawasaki equation

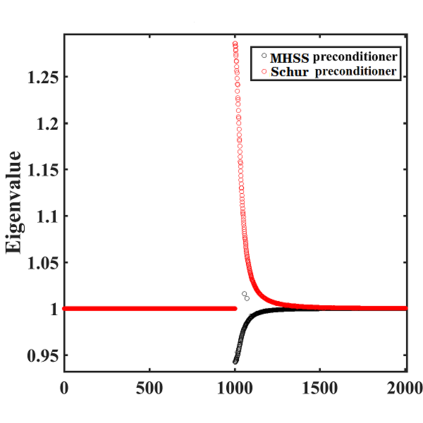
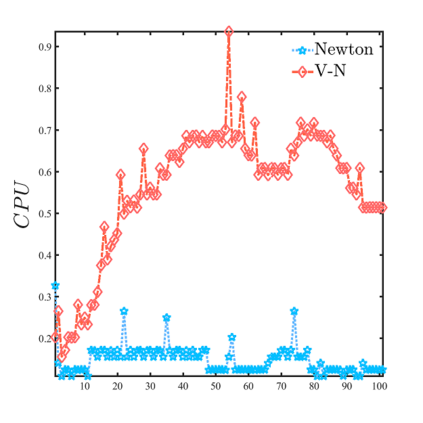
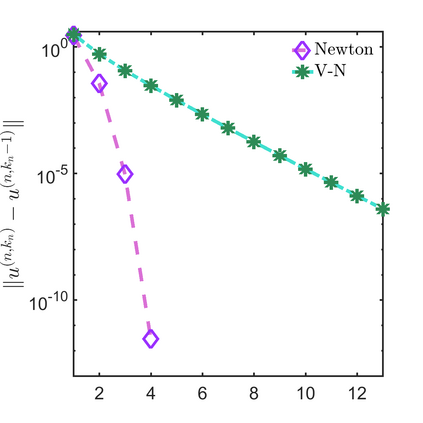
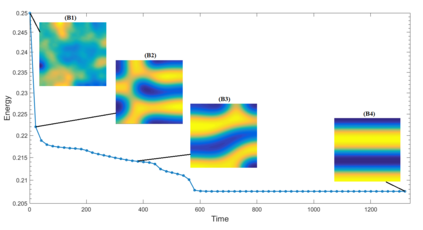
In this paper, we propose a numerical method to solve the mass-conserved Ohta-Kawasaki equation with finite element discretization. An unconditional stable convex split-ting scheme is applied to time approximation. The Newton method and its variant are used to address the implicitly nonlinear term. We rigorously analyze the convergence of the Newton iteration methods. Theoretical results demonstrate that two Newton iteration methods have the same convergence rate, and the Newton method has a smaller convergent factor than the variant one. To reduce the condition number of discretized linear system, we design two efficient block preconditioners and analyze their spectral distribution. Finally, we offer numerical examples to support the theoretical analysis and indicate the efficiency of the proposed numerical methods for the mass-conserved Ohta-Kawasaki equation.