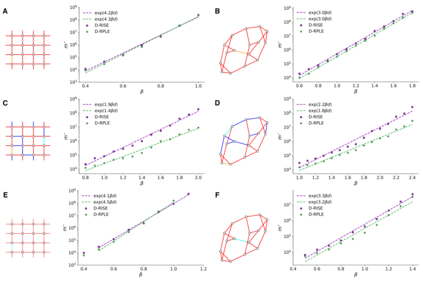
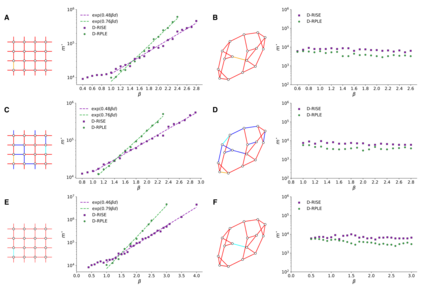
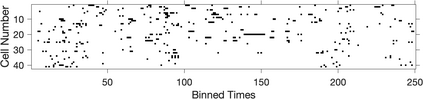
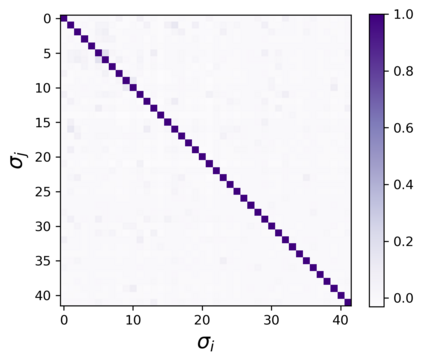
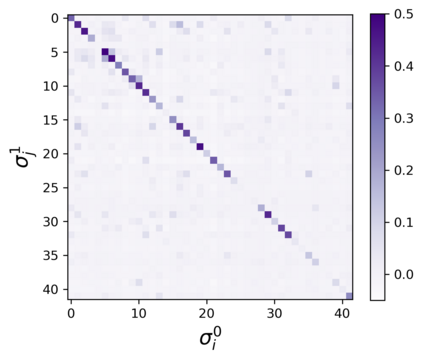
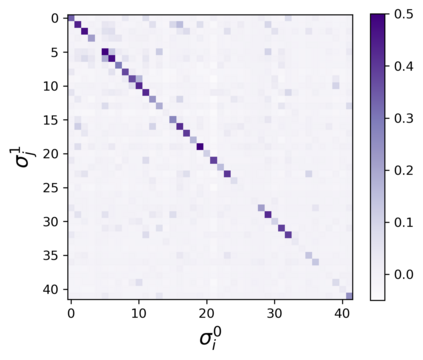
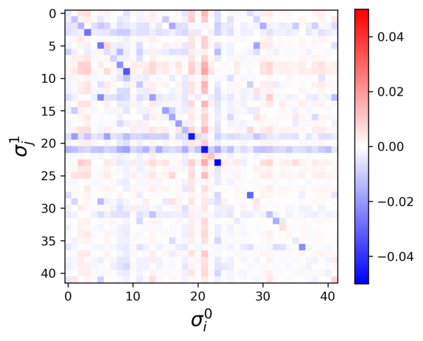
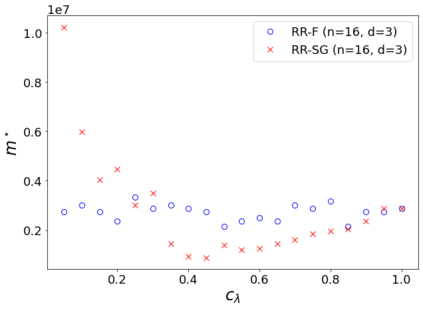
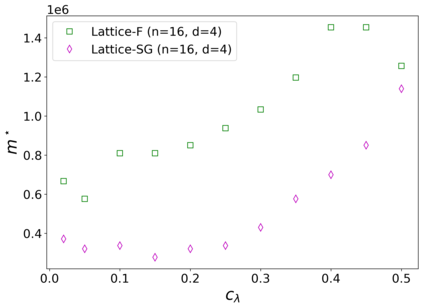
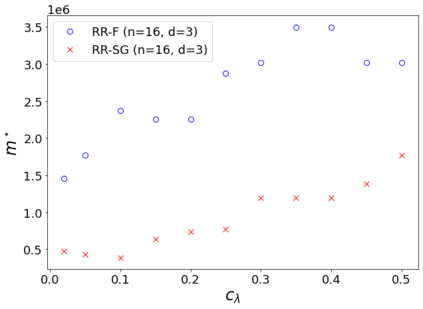
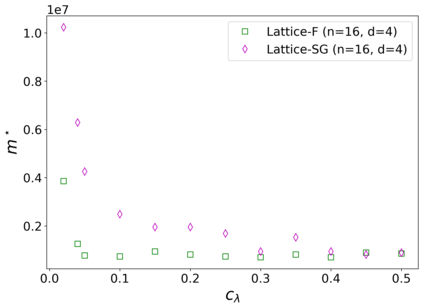
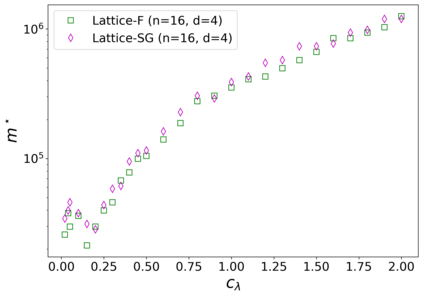
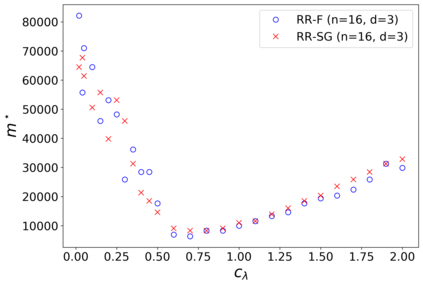
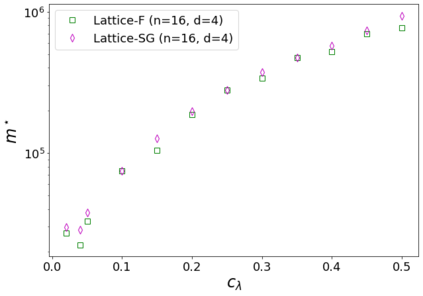
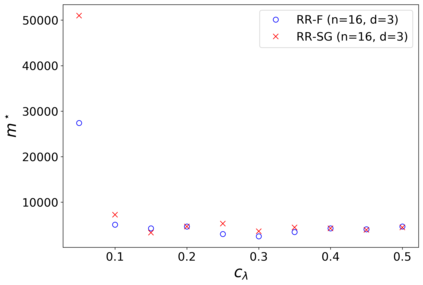
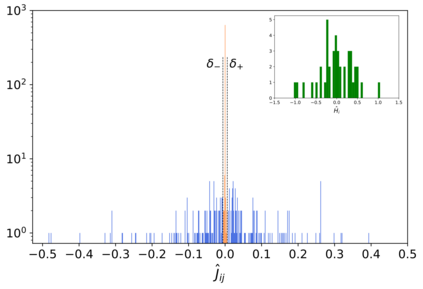
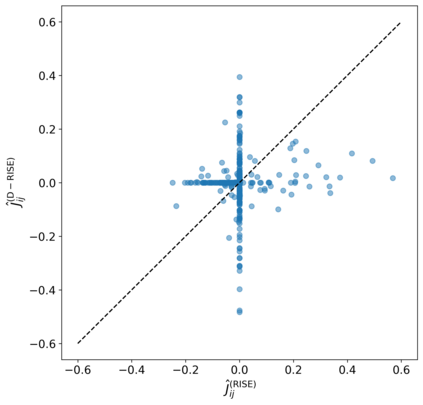
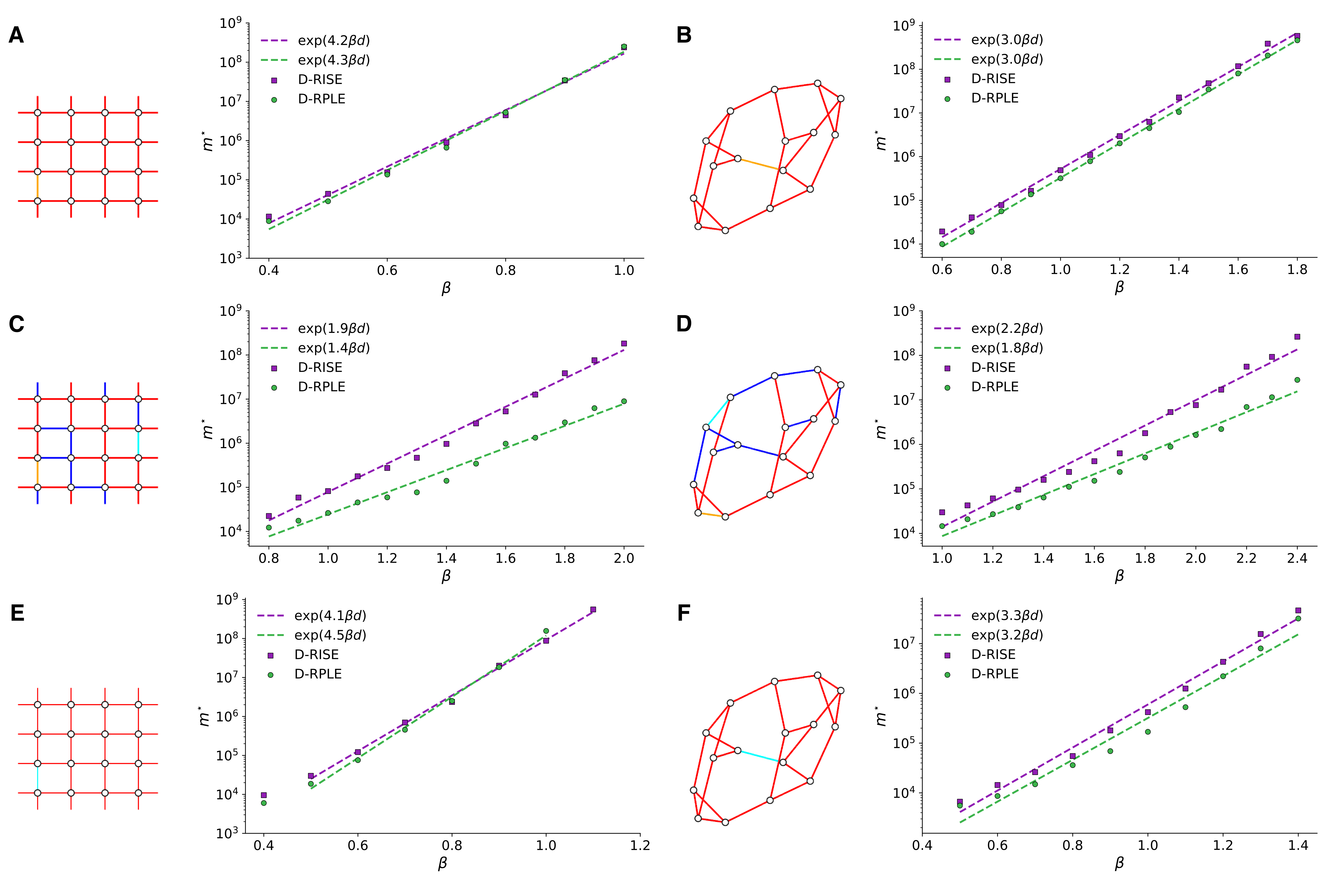
The usual setting for learning the structure and parameters of a graphical model assumes the availability of independent samples produced from the corresponding multivariate probability distribution. However, for many models the mixing time of the respective Markov chain can be very large and i.i.d. samples may not be obtained. We study the problem of reconstructing binary graphical models from correlated samples produced by a dynamical process, which is natural in many applications. We analyze the sample complexity of two estimators that are based on the interaction screening objective and the conditional likelihood loss. We observe that for samples coming from a dynamical process far from equilibrium, the sample complexity reduces exponentially compared to a dynamical process that mixes quickly.
翻译:用于学习图形模型结构和参数的通常设置假设从相应的多变概率分布中产生的独立样本的可用性;然而,对于许多模型来说,各自Markov链条的混合时间可能非常大,而且可能无法获取样本。我们研究了从动态过程产生的相关样本中重建二进制图形模型的问题,在许多应用中,这种动态过程是自然的。我们分析了基于互动筛选目标和有条件可能性损失的两个估计器的样本复杂性。我们观察到,对于远离平衡的动态过程的样本,与快速混合的动态过程相比,样本复杂性指数性下降。