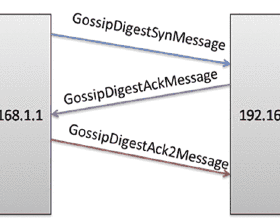
We consider a system with a source which maintains the most current version of a file, and a ring network of $n$ user nodes that wish to acquire the latest version of the file. The source gets updated with newer file versions as a point process, and forwards them to the user nodes, which further forward them to their neighbors using a memoryless gossip protocol. We study the average version age of this network in the presence of $\tilde{n}$ jammers that disrupt inter-node communications. To this purpose, we construct an alternate system model of mini-rings and prove that the version age of the original model can be sandwiched between constant multiples of the version age of the alternate model. We show that when the number of jammers scales as a fractional power of the network size, i.e., $\tilde n= cn^\alpha$, the version age scales as $\sqrt{n}$ when $\alpha < \frac{1}{2}$, and as $n^{\alpha}$ when $\alpha \geq \frac{1}{2}$. As the version age of a ring network without any jammers scales as $\sqrt{n}$, our result implies that the version age with gossiping is robust against up to $\sqrt{n}$ jammers in a ring network.
翻译:我们考虑一个系统,其源码维持的是文件的最新版本,一个由美元用户节点组成的环形网络,希望获取文件的最新版本。源码以更新的版本更新,将其作为一个点进程,并将其转发给用户节点,这些节点使用一个没有记忆的八卦协议将其进一步转发给邻居。我们研究这个网络的平均版本年龄,在$\tilde{n}干扰跨节点通信的干扰器面前。为此,我们建立一个微型环的替代系统模型,并证明原始模型的版本年龄可以在替代模式版本的版本年龄的常数倍数之间被替换。我们显示,当干扰器数量以网络大小的分数为分数,即$\tilde n=cn ⁇ alpha$,当$\qr2} 版本为美元时,当$\qrock_rt%} 和 irms a\\qqqrus 的网络规模,当$\qq\\\\\\\\\xxxxxxxxxxx 的版本时,当 irus typeal typeal__ ir__xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx