Decentralized SGD with Asynchronous, Local and Quantized Updates

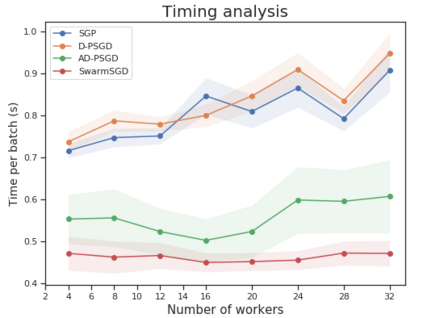
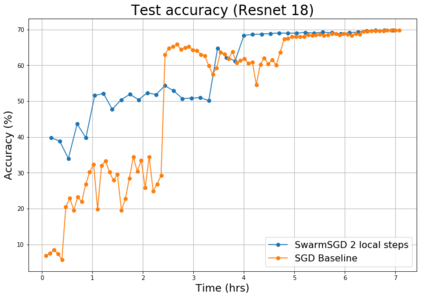
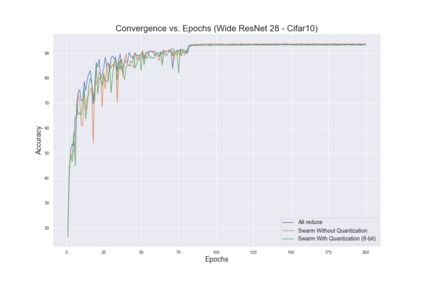
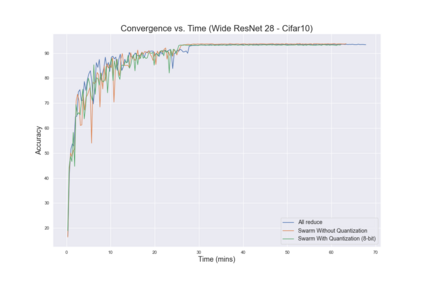
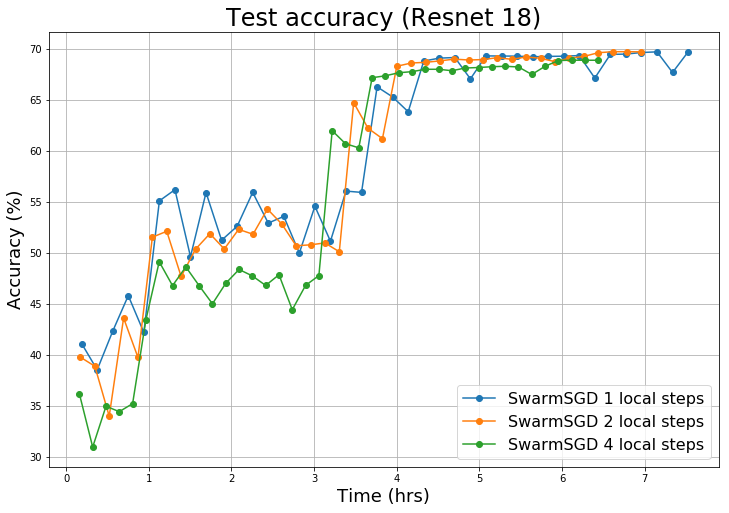
The ability to scale distributed optimization to large node counts has been one of the main enablers of recent progress in machine learning. To this end, several techniques have been explored, such as asynchronous, decentralized, or quantized communication--which significantly reduce the cost of synchronization, and the ability for nodes to perform several local model updates before communicating--which reduces the frequency of synchronization. In this paper, we show that these techniques, which have so far been considered independently, can be jointly leveraged to minimize distribution cost for training neural network models via stochastic gradient descent (SGD). We consider a setting with minimal coordination: we have a large number of nodes on a communication graph, each with a local subset of data, performing independent SGD updates onto their local models. After some number of local updates, each node chooses an interaction partner uniformly at random from its neighbors, and averages a possibly quantized version of its local model with the neighbor's model. Our first contribution is in proving that, even under such a relaxed setting, SGD can still be guaranteed to converge under standard assumptions. The proof is based on a new connection with parallel load-balancing processes, and improves existing techniques by jointly handling decentralization, asynchrony, quantization, and local updates, and by bounding their impact. On the practical side, we implement variants of our algorithm and deploy them onto distributed environments, and show that they can successfully converge and scale for large-scale image classification and translation tasks, matching or even slightly improving the accuracy of previous methods.