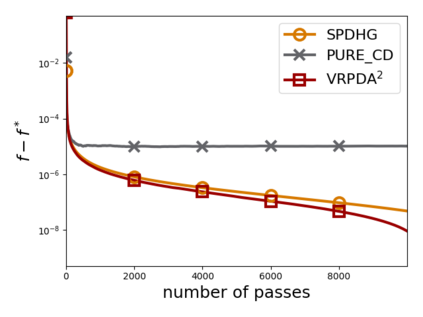
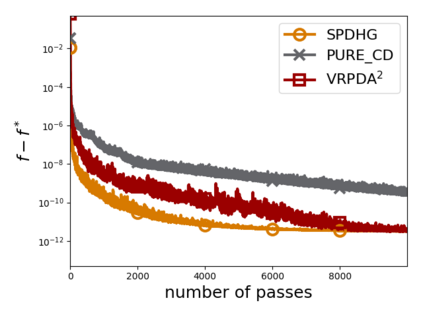
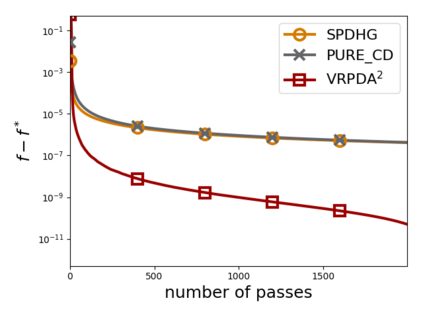
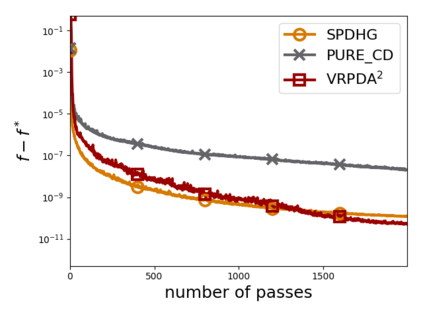
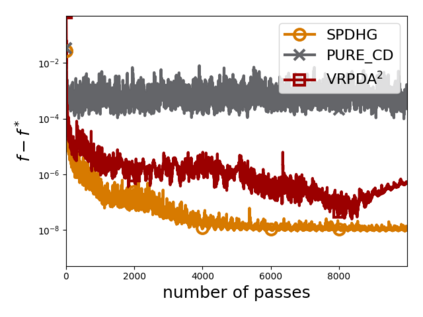
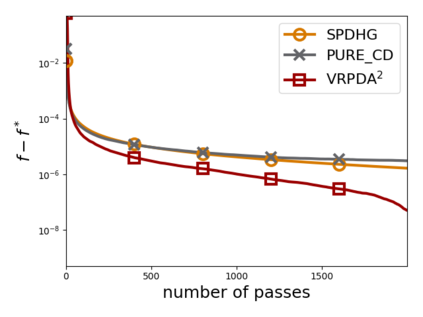
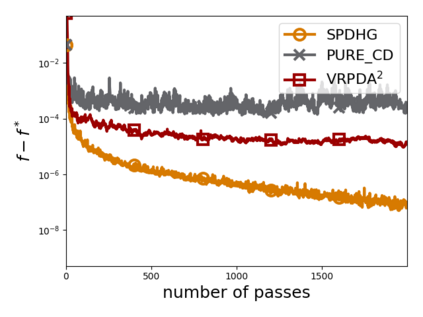
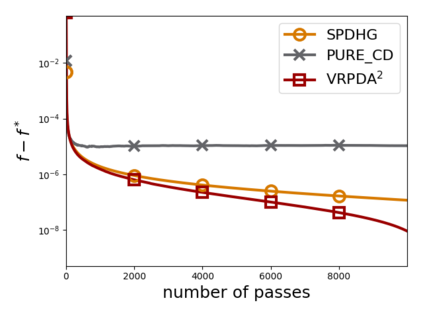
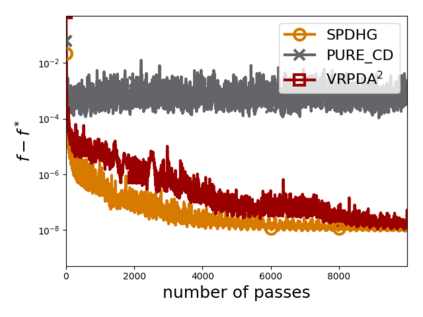
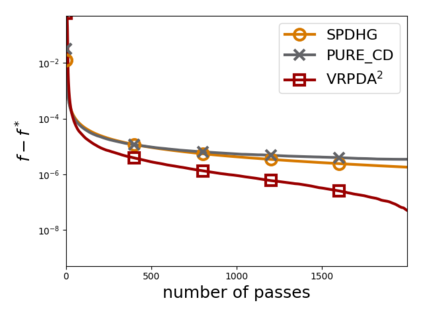
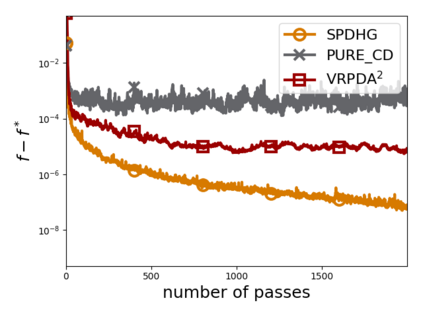
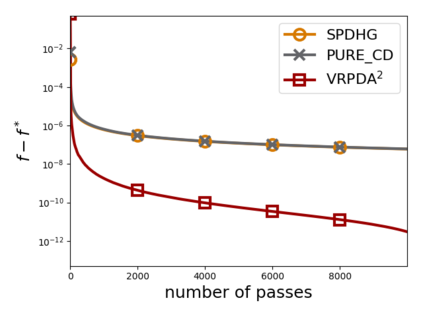
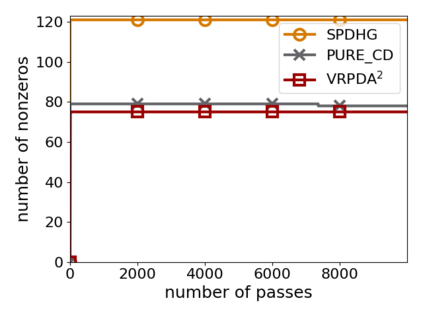
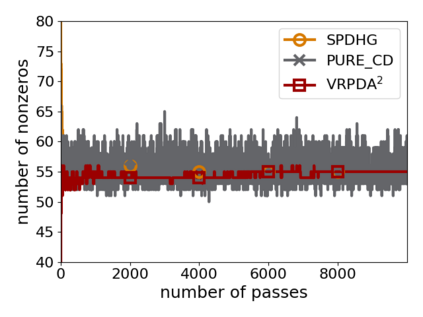
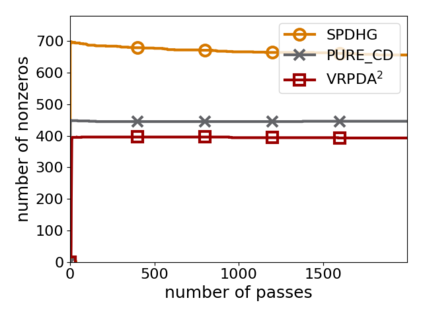
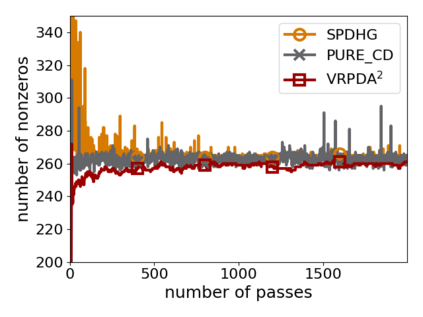
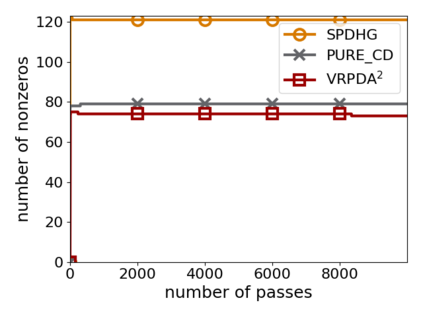
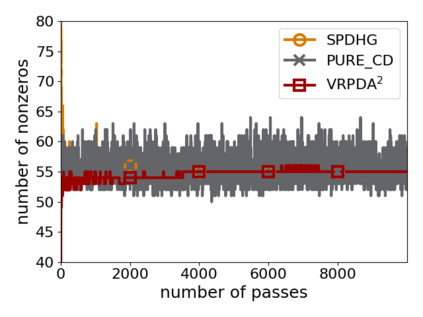
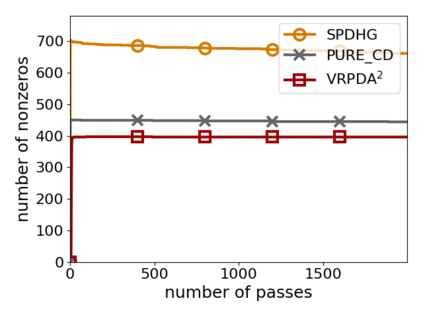
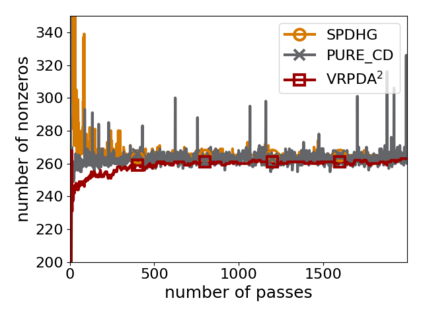
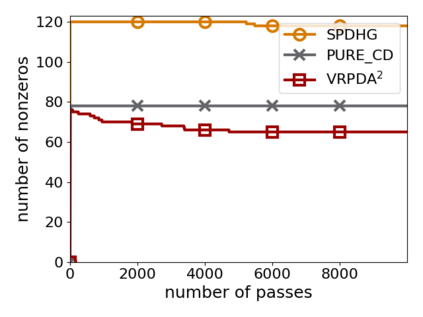
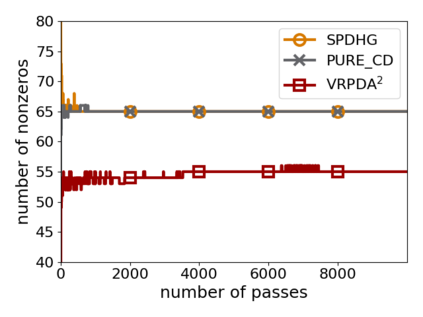
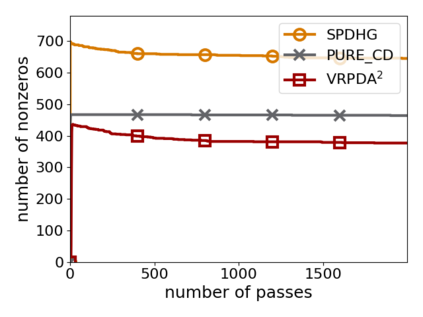
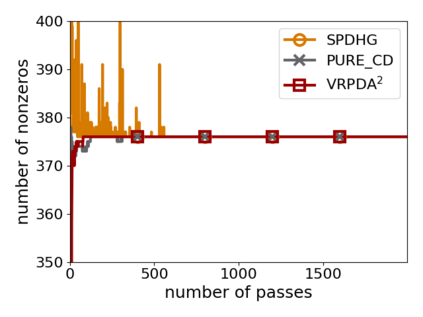
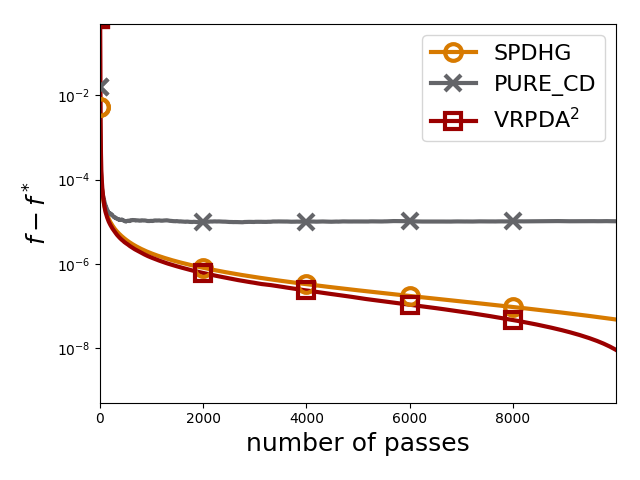
We study structured nonsmooth convex finite-sum optimization that appears widely in machine learning applications, including support vector machines and least absolute deviation. For the primal-dual formulation of this problem, we propose a novel algorithm called \emph{Variance Reduction via Primal-Dual Accelerated Dual Averaging (\vrpda)}. In the nonsmooth and general convex setting, \vrpda~has the overall complexity $O(nd\log\min \{1/\epsilon, n\} + d/\epsilon )$ in terms of the primal-dual gap, where $n$ denotes the number of samples, $d$ the dimension of the primal variables, and $\epsilon$ the desired accuracy. In the nonsmooth and strongly convex setting, the overall complexity of \vrpda~becomes $O(nd\log\min\{1/\epsilon, n\} + d/\sqrt{\epsilon})$ in terms of both the primal-dual gap and the distance between iterate and optimal solution. Both these results for \vrpda~improve significantly on state-of-the-art complexity estimates, which are $O(nd\log \min\{1/\epsilon, n\} + \sqrt{n}d/\epsilon)$ for the nonsmooth and general convex setting and $O(nd\log \min\{1/\epsilon, n\} + \sqrt{n}d/\sqrt{\epsilon})$ for the nonsmooth and strongly convex setting, in a much more simple and straightforward way. Moreover, both complexities are better than \emph{lower} bounds for general convex finite sums that lack the particular (common) structure that we consider. Our theoretical results are supported by numerical experiments, which confirm the competitive performance of \vrpda~compared to state-of-the-art.
翻译:我们研究在机器学习应用程序中出现的结构化非moot convex 限制和优化, 包括支持矢量机和最小绝对偏差。 对于这个问题的原始- 双向配方配方, 我们提议了一个叫做\ emph{ 减少通过纯- 双加速双重变异( vrpda) 的新型算法。 在非移动和一般的 convex 设置中,\ vrpda~ 具有总体复杂性 $ (nd\log\ min\ 1/\\\\ epsilon, n\ + d/ d/ epsilon ), 在初始- 介质差异上, $ 表示样本的数量, $ 初等变量的尺寸, $, 和 $\ complex 的精度定序。 在非移动和离子结构中, 以( nq\\\ d==x) 的内, 内基值和内基值的内基值和内基值的内基值 。