Capacity Achieving by Diagonal Permutation for MU-MIMO channels

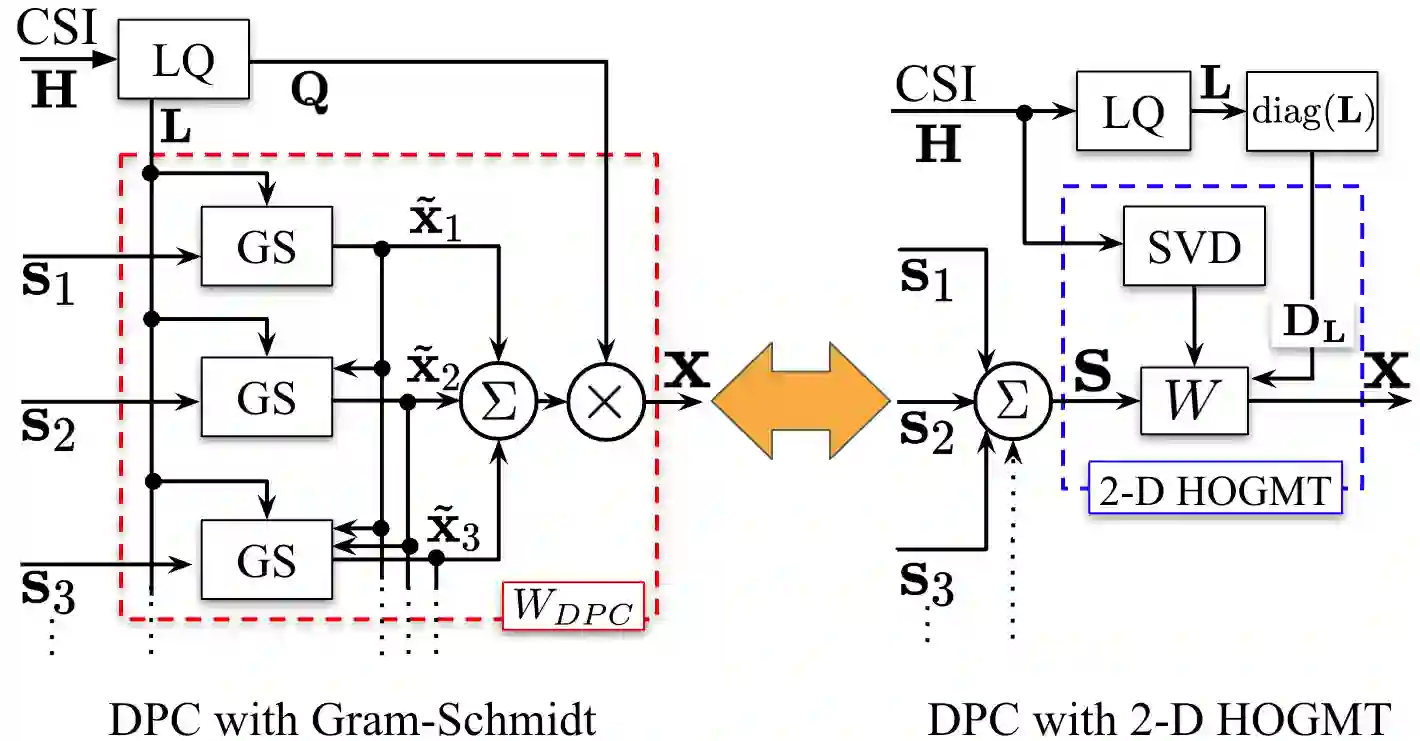
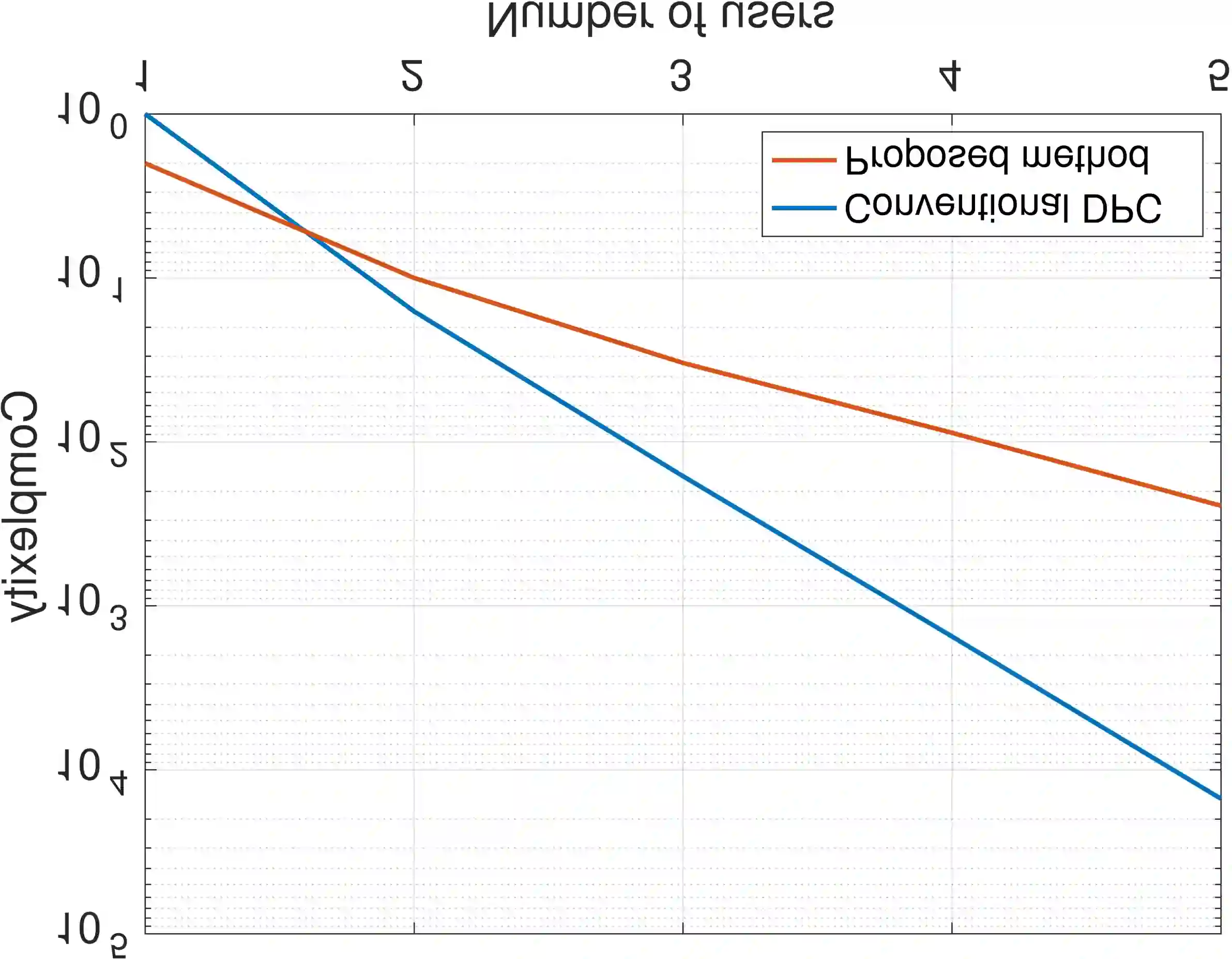
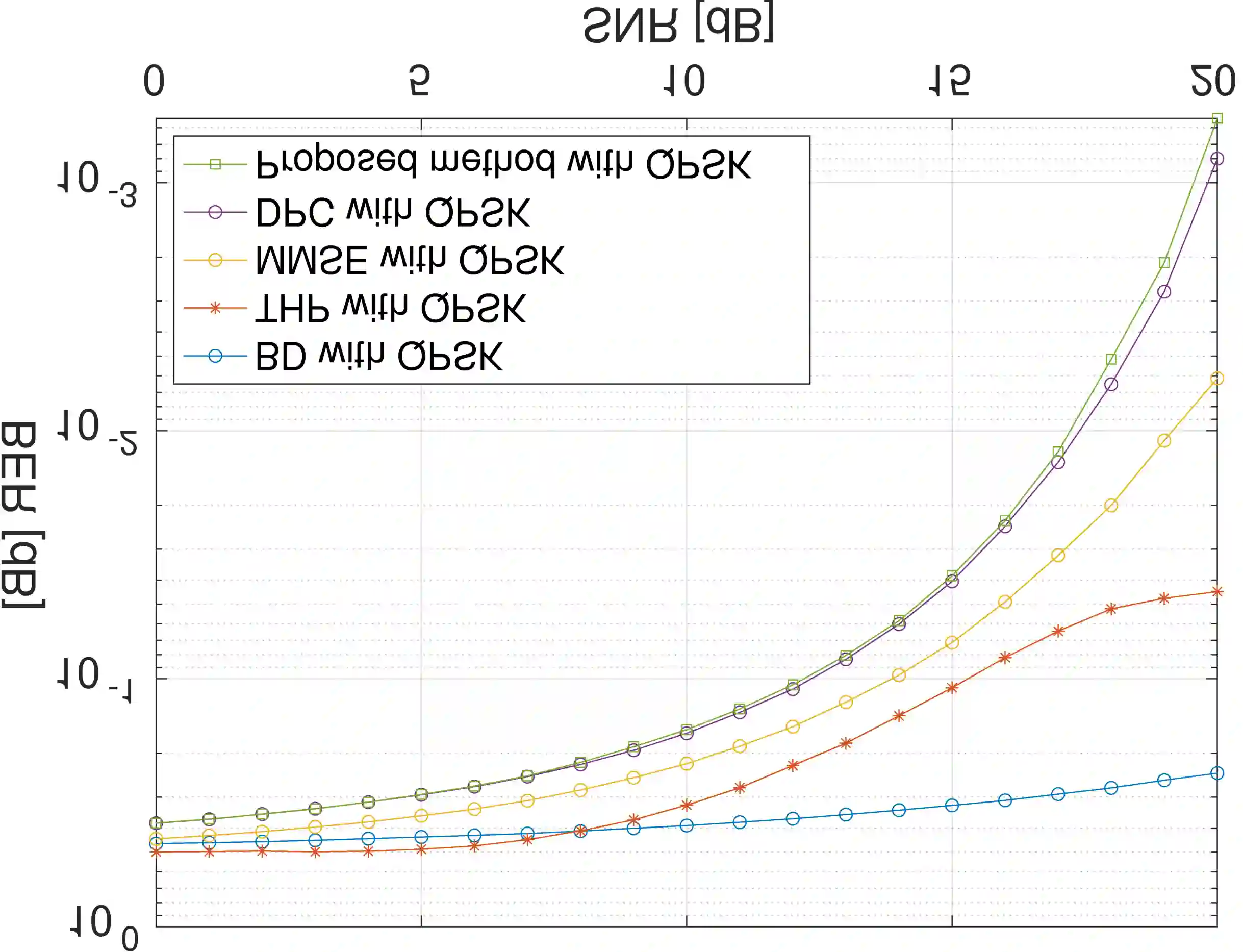
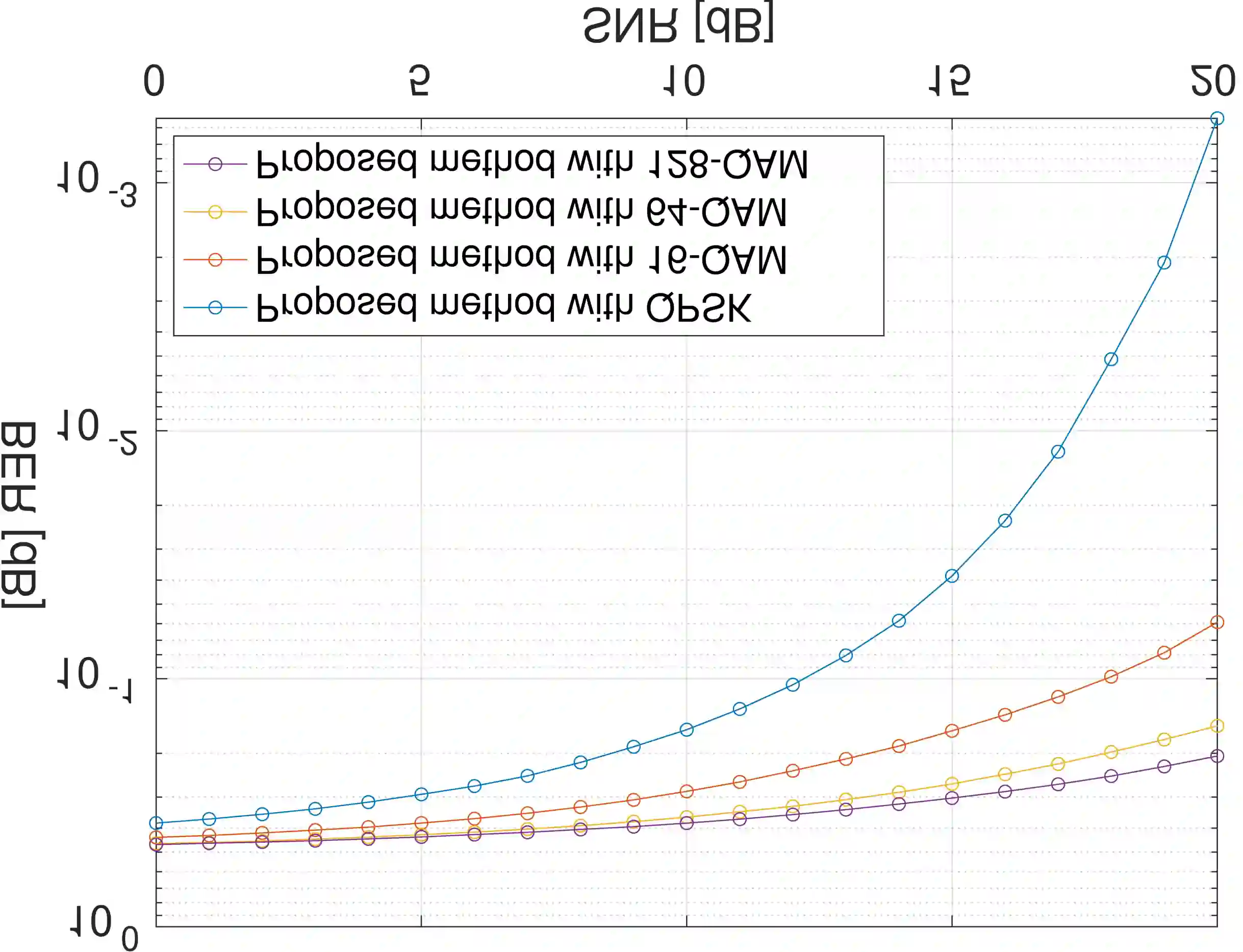
Dirty Paper Coding (DPC) is considered as the optimal precoding which achieves capacity for the Gaussian Multiple-Input Multiple-Output (MIMO) broadcast channel (BC). However, to find the optimal precoding order, it needs to repeat N! times for N users as there are N! possible precoding orders. This extremely high complexity limits its practical use in modern wireless networks. In this paper, we show the equivalence of DPC and the recently proposed Higher Order Mercer's Theorem (HOGMT) precoding[1][2] in 2-D (spatial) case, which provides an alternate implementation for DPC. Furthermore, we show that the proposed implementation method is linear over the permutation operator when permuting over multi-user channels. Therefore, we present a low complexity algorithm that optimizes the precoding order for DPC with beamforming, eliminating repeated computation of DPC for each precoding order. Simulations show that our method can achieve the same result as conventional DPC with about 20 dB lower complexity for N = 5 users.