Optimal Bayesian Quickest Detection for Hidden Markov Models and Structured Generalisations

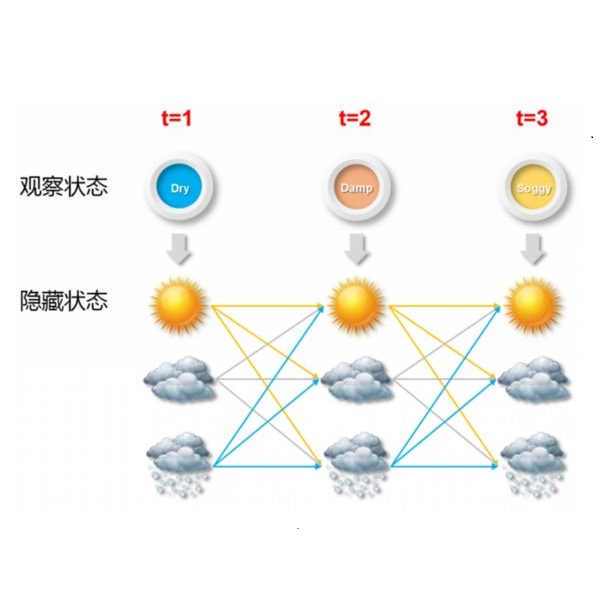
In this paper we consider the problem of quickly detecting changes in hidden Markov models (HMMs) in a Bayesian setting, as well as several structured generalisations including changes in statistically periodic processes, quickest detection of a Markov process across a sensor array, quickest detection of a moving target in a sensor network and quickest change detection (QCD) in multistream data. Our main result establishes an optimal Bayesian HMM QCD rule with a threshold structure. This framework and proof techniques allow us to elegantly establish optimal rules for the structured generalisations by showing that these problems are special cases of the Bayesian HMM QCD problem. The threshold structure enables us to develop bounds to characterise the performance of our optimal rule and provide an efficient method for computing the test statistic. Finally, we examine the performance of our rule in several simulation examples and propose a technique for calculating the optimal threshold.