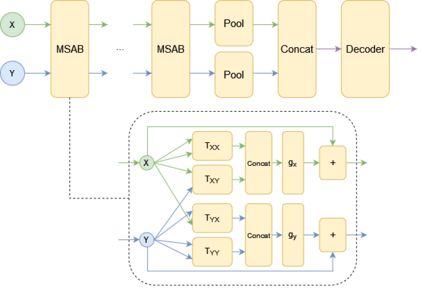
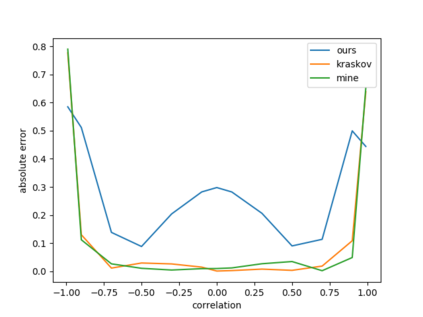
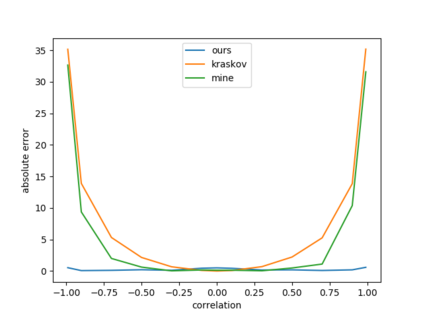
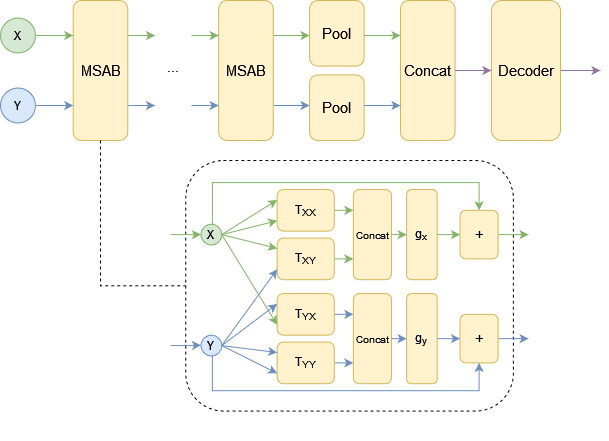
We propose a general deep architecture for learning functions on multiple permutation-invariant sets. We also show how to generalize this architecture to sets of elements of any dimension by dimension equivariance. We demonstrate that our architecture is a universal approximator of these functions, and show superior results to existing methods on a variety of tasks including counting tasks, alignment tasks, distinguishability tasks and statistical distance measurements. This last task is quite important in Machine Learning. Although our approach is quite general, we demonstrate that it can generate approximate estimates of KL divergence and mutual information that are more accurate than previous techniques that are specifically designed to approximate those statistical distances.
翻译:我们提出一个通用的深层架构,用于在多变-异变组合中学习功能。 我们还展示了如何将这一架构概括为按大小等同度排列的任何层面要素组。 我们展示了我们的架构是这些功能的通用近似体,并展示了优于现有方法的各种任务,包括计数任务、调整任务、区别任务和统计距离测量等现有方法的优异效果。 最后一项任务在机器学习中相当重要。 尽管我们的方法相当笼统,但我们证明它能够产生对KL差异的大致估计,以及比以往专门设计来估计这些统计距离的技术更准确的相互信息。