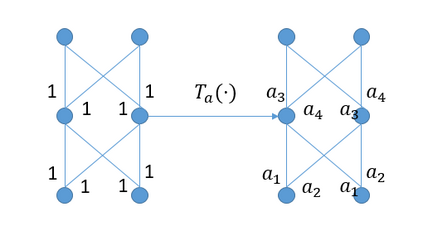
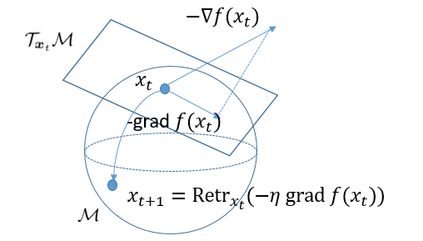
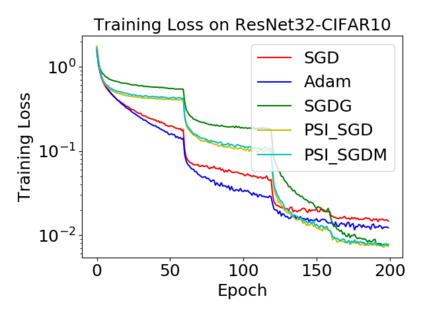
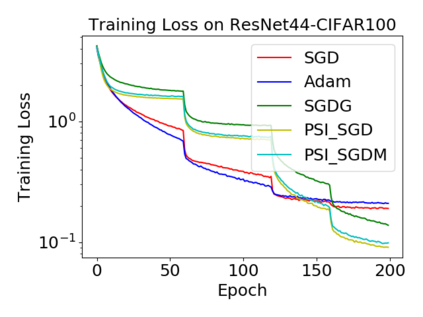
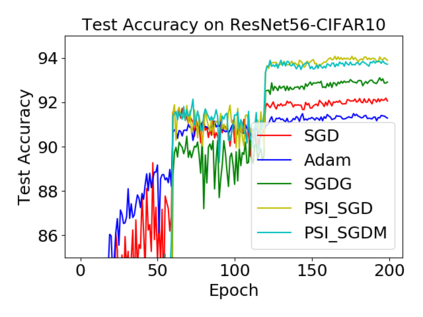
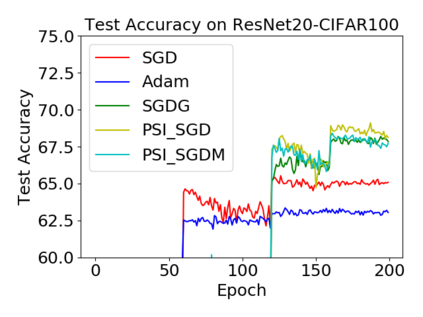
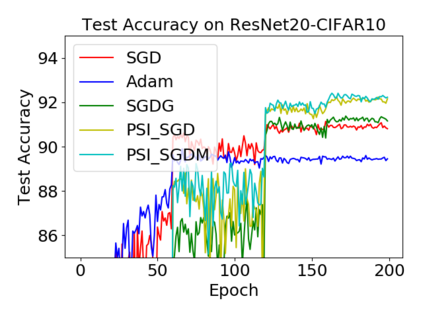
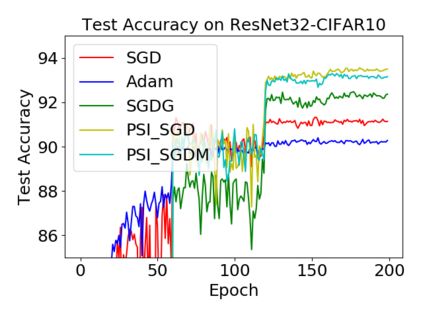
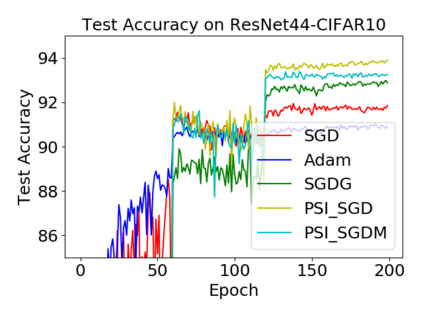
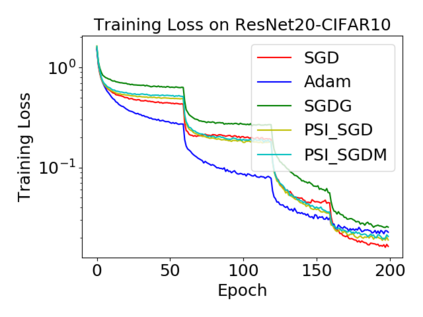
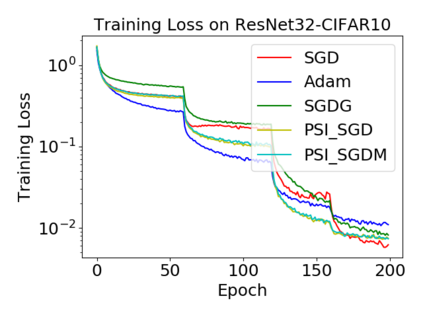
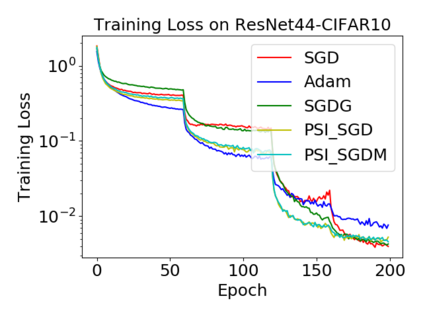
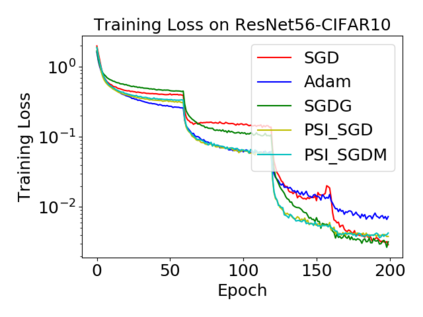
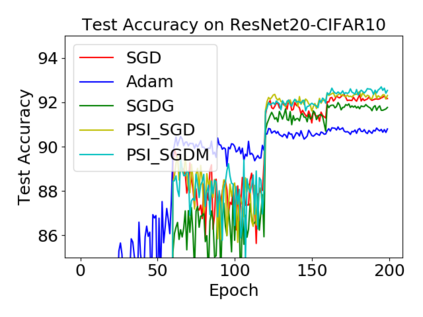
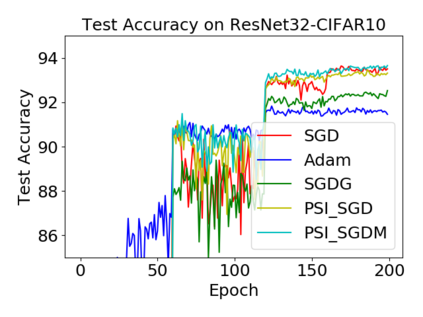
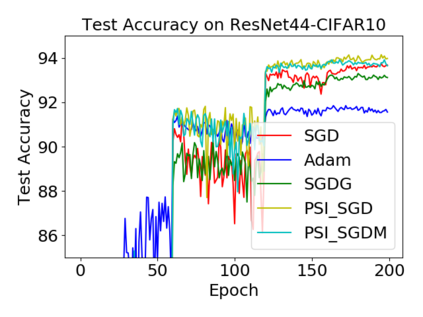
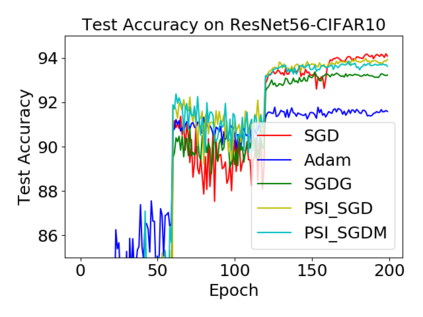
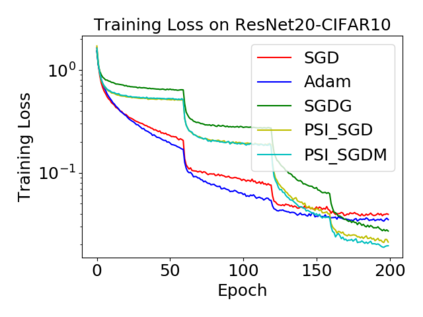
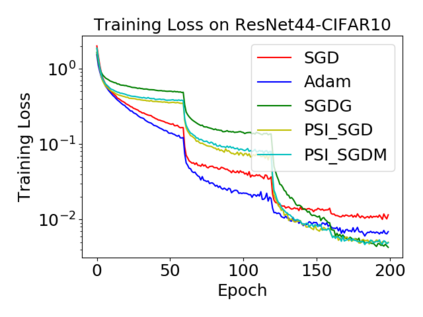
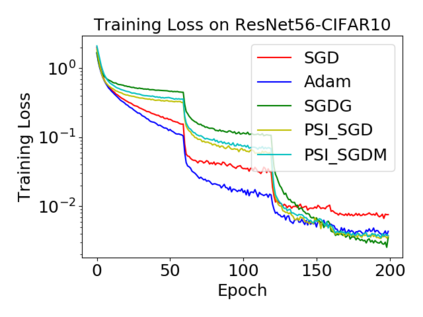
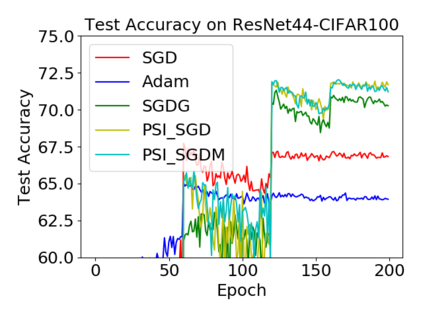
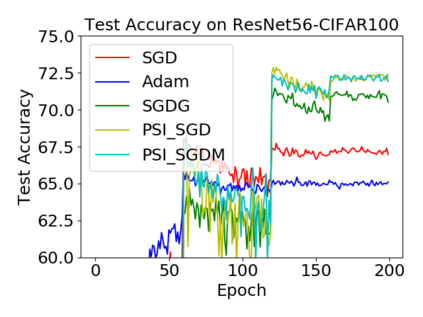
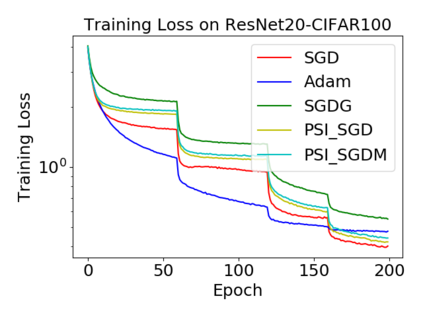
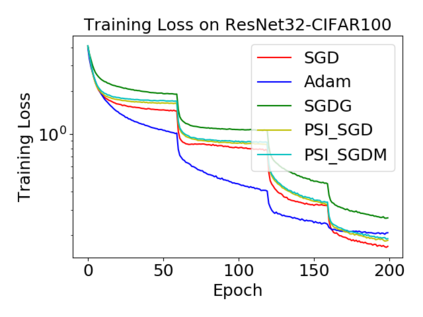
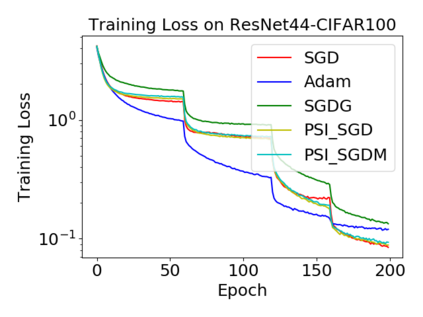
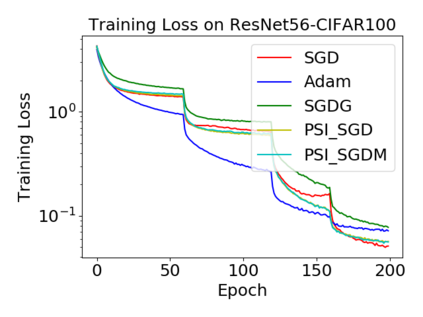
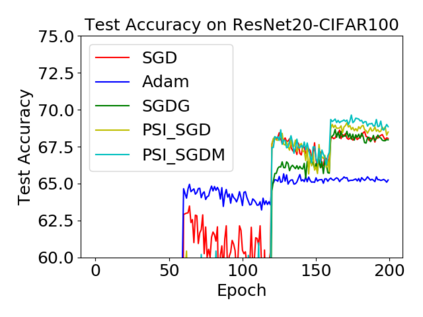
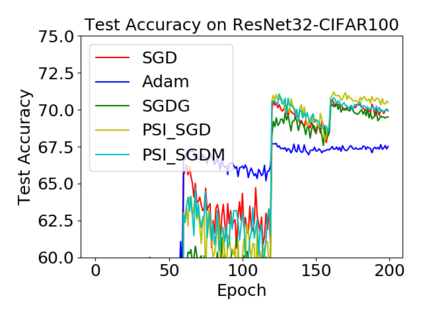
Batch normalization (BN) has become a crucial component across diverse deep neural networks. The network with BN is invariant to positively linear re-scaling of weights, which makes there exist infinite functionally equivalent networks with various scales of weights. However, optimizing these equivalent networks with the first-order method such as stochastic gradient descent will converge to different local optima owing to different gradients across training. To alleviate this, we propose a quotient manifold \emph{PSI manifold}, in which all the equivalent weights of the network with BN are regarded as the same one element. Then, gradient descent and stochastic gradient descent on the PSI manifold are also constructed. The two algorithms guarantee that every group of equivalent weights (caused by positively re-scaling) converge to the equivalent optima. Besides that, we give the convergence rate of the proposed algorithms on PSI manifold and justify that they accelerate training compared with the algorithms on the Euclidean weight space. Empirical studies show that our algorithms can consistently achieve better performances over various experimental settings.
翻译:批量正常化(BN) 已成为不同深度神经网络的一个关键组成部分。 BN 的网络对正线性重缩缩放不起作用, 这使得存在无限的功能等效网络, 其重量范围各异。 然而, 优化这些等效网络, 使用第一等方法( 如随机梯度梯度下降) 将聚集到不同的本地选取中 。 为了减轻这一影响, 我们建议使用一个商数式的多元元 \ emph{ PSI 倍数}, 其中BN 的网络的所有等值重量都被视为同一个元素 。 然后, PSI 元的梯度下行和随机梯度梯度下行也构建了。 两种算法保证了每组等等重量( 由积极的再缩放导致的) 都与同等的选取方法相趋同。 此外, 我们给出了PSI 多重算法的趋同率的趋同率率, 并证明它们与 Euclidean 重量空间的算法相比加速了培训。 Eprialalalal 研究表明, 我们的算算算法可以持续地在各种实验环境中取得更好的表现。