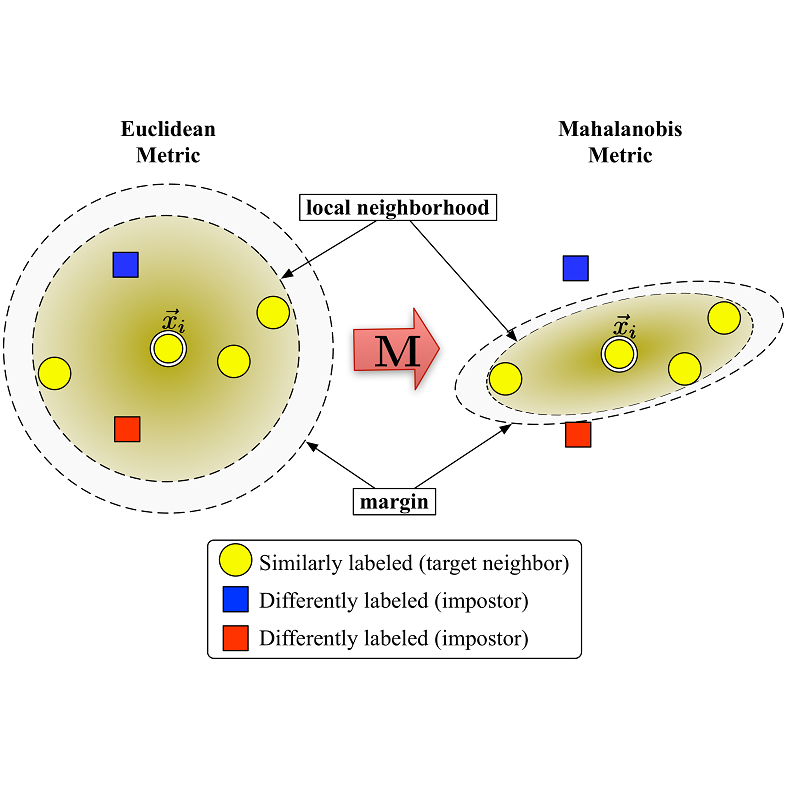
Metric learning aims to learn a distance metric such that semantically similar instances are pulled together while dissimilar instances are pushed away. Many existing methods consider maximizing or at least constraining a distance margin in the feature space that separates similar and dissimilar pairs of instances to guarantee their generalization ability. In this paper, we advocate imposing an adversarial margin in the input space so as to improve the generalization and robustness of metric learning algorithms. We first show that, the adversarial margin, defined as the distance between training instances and their closest adversarial examples in the input space, takes account of both the distance margin in the feature space and the correlation between the metric and triplet constraints. Next, to enhance robustness to instance perturbation, we propose to enlarge the adversarial margin through minimizing a derived novel loss function termed the perturbation loss. The proposed loss can be viewed as a data-dependent regularizer and easily plugged into any existing metric learning methods. Finally, we show that the enlarged margin is beneficial to the generalization ability by using the theoretical technique of algorithmic robustness. Experimental results on 16 datasets demonstrate the superiority of the proposed method over existing state-of-the-art methods in both discrimination accuracy and robustness against possible noise.
翻译:计量学习的目的是学习一种远程测量,这样可以将精密相似的情况结合在一起,同时将不同的情况推开。许多现有方法考虑最大限度地或至少限制特征空间的距离差,将相似和不同的情况区分开来,以保障其普遍性能力。在本文件中,我们主张在输入空间中设置对抗差,以改进计量学习算法的概括性和稳健性。我们首先表明,将培训实例与其在输入空间中最接近的对抗实例的距离定义为敌对差,考虑到地物空间的距离差以及衡量和三重限制的相互关系。接下来,为了增强实例的稳健度,我们提议通过尽量减少称为扰动损失的新颖损失功能来扩大对抗差。提议的损失可被视为依赖数据的调节器,并容易地插入任何现有的计量学习方法。最后,我们表明,扩大的差幅通过使用逻辑稳健的理论技术,有利于普遍化能力。16个数据定位的实验结果显示,与现有方法的稳健性相比,现有方法的稳健性是优劣性。