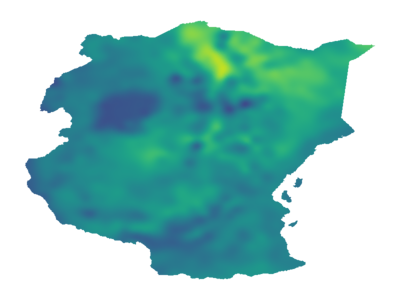
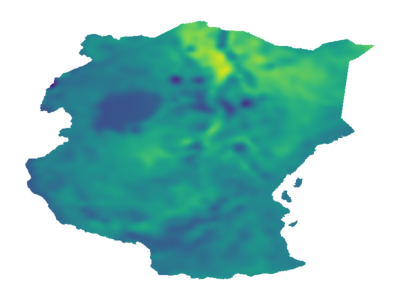
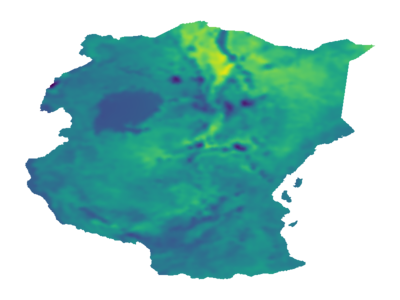
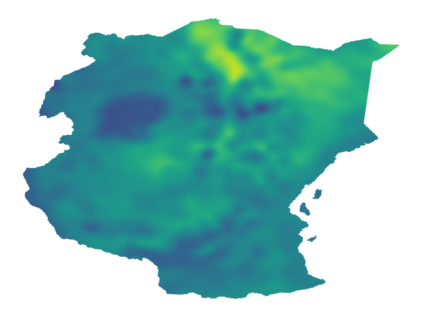
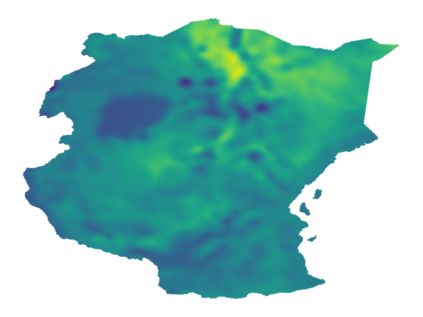
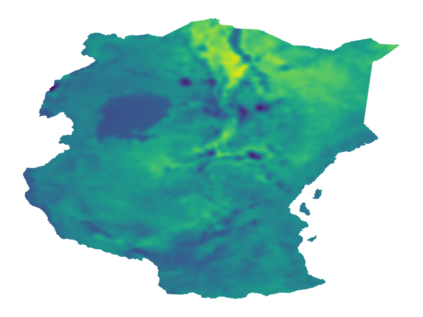
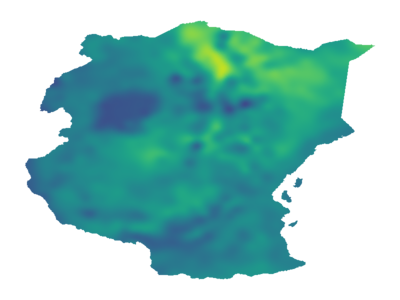
As Gaussian processes mature, they are increasingly being deployed as part of larger machine learning and decision-making systems, for instance in geospatial modeling, Bayesian optimization, or in latent Gaussian models. Within a system, the Gaussian process model needs to perform in a stable and reliable manner to ensure it interacts correctly with other parts the system. In this work, we study the numerical stability of scalable sparse approximations based on inducing points. We derive sufficient and in certain cases necessary conditions on the inducing points for the computations performed to be numerically stable. For low-dimensional tasks such as geospatial modeling, we propose an automated method for computing inducing points satisfying these conditions. This is done via a modification of the cover tree data structure, which is of independent interest. We additionally propose an alternative sparse approximation for regression with a Gaussian likelihood which trades off a small amount of performance to further improve stability. We evaluate the proposed techniques on a number of examples, showing that, in geospatial settings, sparse approximations with guaranteed numerical stability often perform comparably to those without.
翻译:随着高斯进程成熟,它们正越来越多地作为更大的机器学习和决策系统的一部分被部署,例如在地理空间模型、巴伊西亚优化或潜潜高斯模型中。在一个系统中,高斯进程模型需要以稳定和可靠的方式运行,以确保它与系统其他部分的正确互动。在这项工作中,我们根据诱导点研究可缩放的稀释近似数的数字稳定性。我们从计算数字稳定的引点获得足够和在某些情况下必要的条件。对于诸如地理空间模型等低维度任务,我们提出了计算满足这些条件的诱导点的自动化方法。这是通过修改覆盖树数据结构来完成的,这是独立感兴趣的。我们另外还提出了一种微弱的回归近似数,用少量性能交换微量的性能来进一步改善稳定性。我们从一些例子中评估了拟议的技术,表明在地理空间环境中,有保障数字稳定性的稀释近似数往往与没有这种能力的人相匹配。