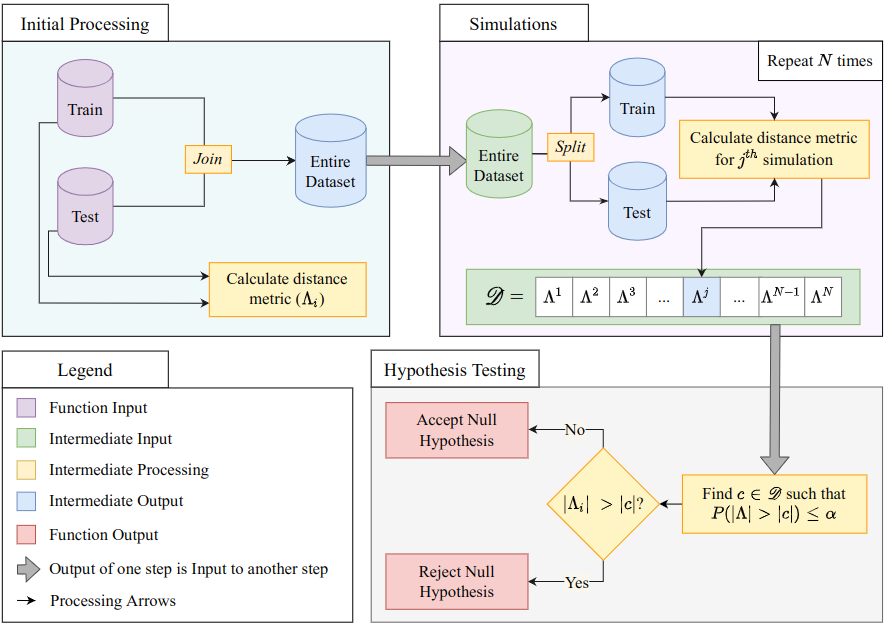
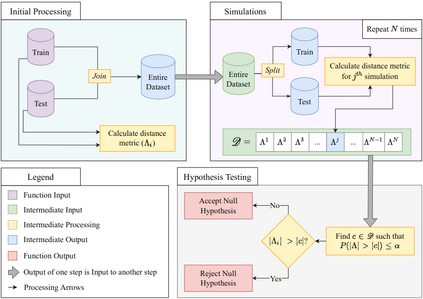
In machine learning, a routine practice is to split the data into a training and a test data set. A proposed model is built based on the training data, and then the performance of the model is assessed using test data. Usually, the data is split randomly into a training and a test set on an ad hoc basis. This approach, pivoted on random splitting, works well but more often than not, it fails to gauge the generalizing capability of the model with respect to perturbations in the input of training and test data. Experimentally, this sensitive aspect of randomness in the input data is realized when a new iteration of a fixed pipeline, from model building to training and testing, is executed, and an overly optimistic performance estimate is reported. Since the consistency in a model's performance predominantly depends on the data splitting, any conclusions on the robustness of the model are unreliable in such a scenario. We propose a diagnostic approach to quantitatively assess the quality of a given split in terms of its true randomness, and provide a basis for inferring model insensitivity towards the input data. We associate model robustness with random splitting using a self-defined data-driven distance metric based on the Mahalanobis squared distance between a train set and its corresponding test set. The probability distribution of the distance metric is simulated using Monte Carlo simulations, and a threshold is calculated from one-sided hypothesis testing. We motivate and showcase the performance of the proposed approach using various real data sets. We also compare the performance of the existing data splitting methods using the proposed method.
翻译:在机器学习中,通常的做法是将数据分成培训和测试数据组,将数据分为培训和测试数据组。根据培训数据构建了一个拟议的模型,然后用测试数据对模型的性能进行评估。通常,数据随机地分为培训和临时测试组。这种方法以随机分解为分流,效果良好,但往往不能衡量模型在干扰培训和测试数据输入方面的总体能力。实验中,如果执行从模型建设到培训和测试的固定管道新迭代,然后用测试来评估模型的性能,然后对模型的性能进行评估。由于模型性能的一致性主要取决于数据分解,因此在这种假设中,任何关于模型稳健性的结论都不可靠。我们提出一种诊断性方法,从数量上评估某项差异在建议的真正随机性与测试和测试数据输入数据中的质量。我们还提出一种推断模型对投入数据的敏感性的基础。我们将模型的稳健性和随机性与使用自己定义的距离数据分级数据分级标准,使用自己定义的数据分级标准标准标准测试。我们用一个自定义的模型和标准级的模拟标准标准测试方法来计算。