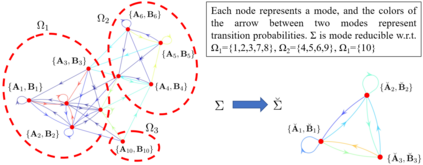
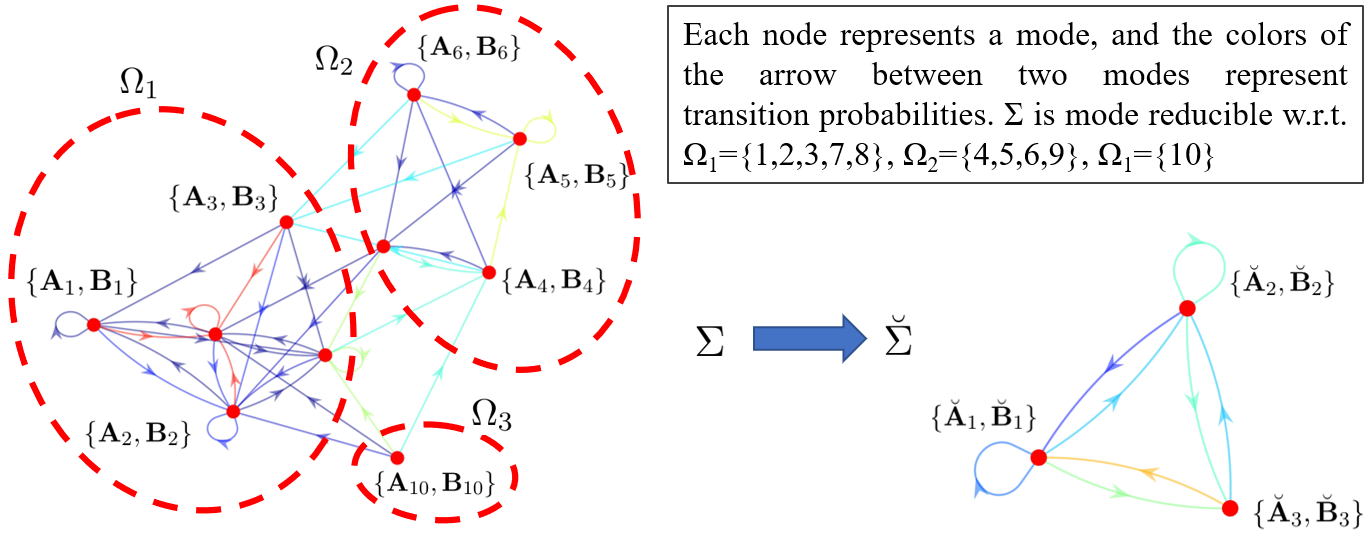
Switched systems are capable of modeling processes with underlying dynamics that may change abruptly over time. To achieve accurate modeling in practice, one may need a large number of modes, but this may in turn increase the model complexity drastically. Existing work on reducing system complexity mainly considers state space reduction, yet reducing the number of modes is less studied. In this work, we consider Markov jump linear systems (MJSs), a special class of switched systems where the active mode switches according to a Markov chain, and several issues associated with its mode complexity. Specifically, inspired by clustering techniques from unsupervised learning, we are able to construct a reduced MJS with fewer modes that approximates well the original MJS under various metrics. Furthermore, both theoretically and empirically, we show how one can use the reduced MJS to analyze stability and design controllers with significant reduction in computational cost while achieving guaranteed accuracy.
翻译:切换的系统能够建模过程,其基本动态可能随时间而突变。为了在实践上实现精确的建模,可能需要大量模式,但这反过来又可能大大增加模型的复杂性。降低系统复杂性的现有工作主要考虑国家空间的缩小,但减少模式数量的研究较少。在这项工作中,我们认为Markov 跳跃线性系统(MJS)是一个特殊的交换系统类别,根据Markov 链条进行主动模式开关,以及与其模式复杂性有关的若干问题。 具体地说,在未受监督的学习组合技术的启发下,我们能够在各种尺度下以更接近原始MJS的较少模式构建一个缩小的MJS。 此外,在理论上和实验上,我们展示了如何利用降低的MJS来分析稳定性和设计控制器,同时大幅降低计算成本,同时实现保证准确性。