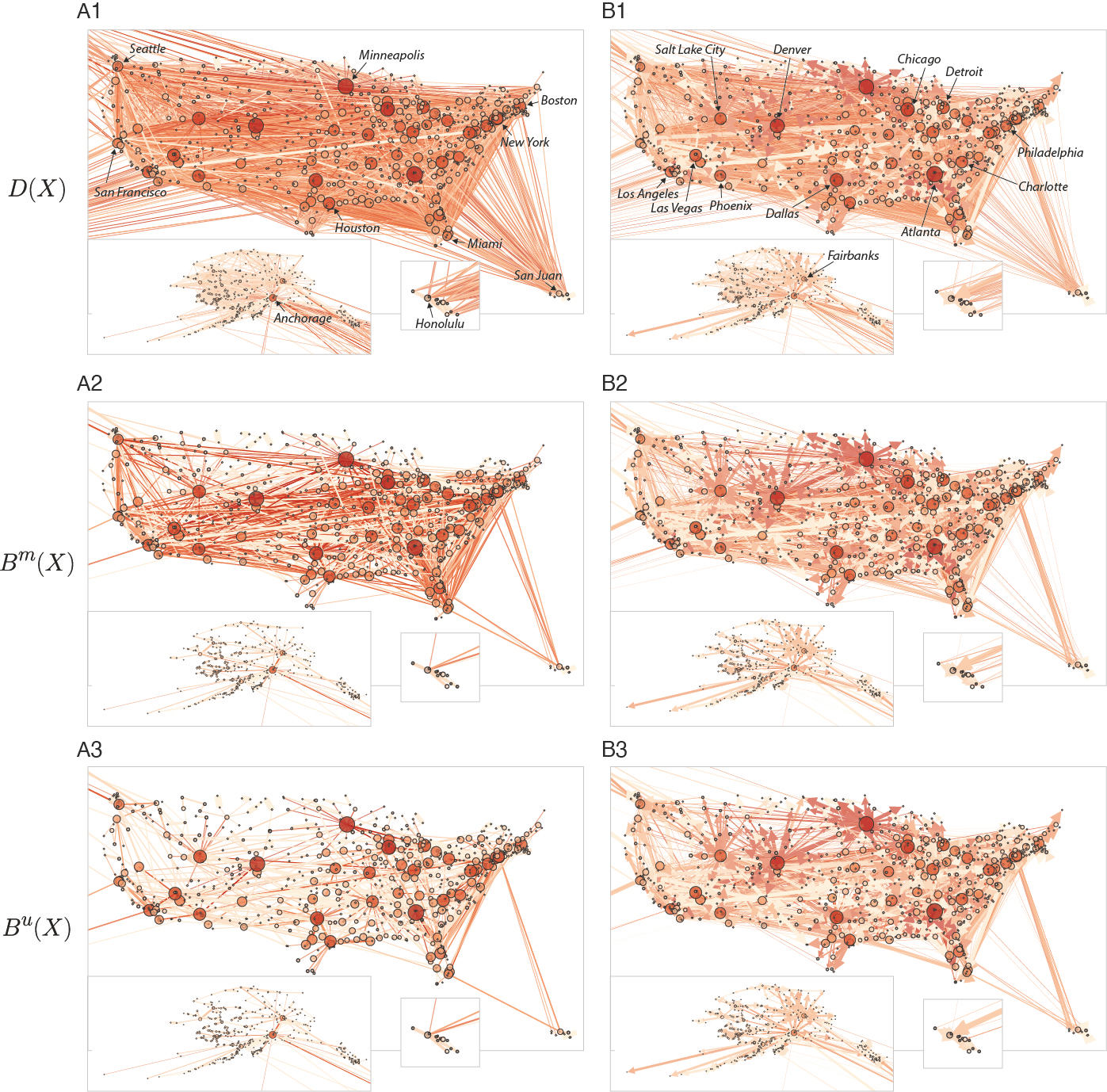
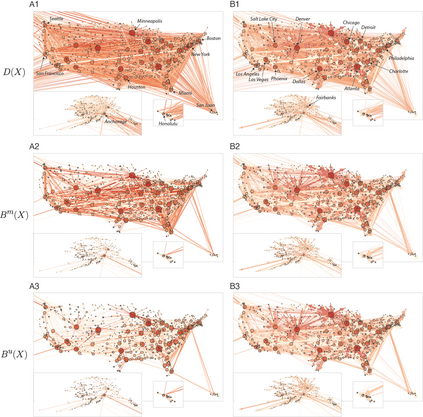
In weighted graphs the shortest path between two nodes is often reached through an indirect path, out of all possible connections, leading to structural redundancies which play key roles in the dynamics and evolution of complex networks. We have previously developed a parameter-free, algebraically-principled methodology to uncover such redundancy and reveal the distance backbone of weighted graphs, which has been shown to be important in transmission dynamics, inference of important paths, and quantifying the robustness of networks. However, the method was developed for undirected graphs. Here we expand this methodology to weighted directed graphs and study the redundancy and robustness found in nine networks ranging from social, biomedical, and technical systems. We found that similarly to undirected graphs, directed graphs in general also contain a large amount of redundancy, as measured by the size of their (directed) distance backbone. Our methodology adds an additional tool to the principled sparsification of complex networks and the measure of their robustness.
翻译:在加权图表中,两个节点之间的最短路径往往通过间接路径,从所有可能的连接中达到,导致结构冗余,在复杂网络的动态和演变中发挥关键作用。我们以前已经开发出一种无参数、代数原则的方法,以发现这种冗余并揭示加权图表的距离主干柱,这在传输动态、重要路径的推论和网络的稳健度方面都很重要。然而,该方法是为非定向图形开发的。我们在这里将这一方法扩大到加权定向图表,并研究从社会、生物医学和技术系统等九个网络中发现的冗余性和稳健性。我们发现,与非定向图表一样,定向图表一般也包含大量冗余,以其(定向)距离主干柱的大小来衡量。我们的方法为复杂网络的有原则的宽度及其坚固度增加了额外的工具。