A Modern Introduction to Online Learning

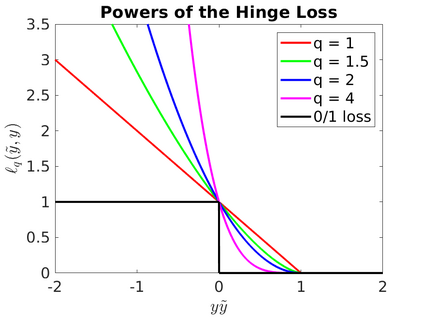
In this monograph, I introduce the basic concepts of Online Learning through a modern view of Online Convex Optimization. Here, online learning refers to the framework of regret minimization under worst-case assumptions. I present first-order and second-order algorithms for online learning with convex losses, in Euclidean and non-Euclidean settings. All the algorithms are clearly presented as instantiation of Online Mirror Descent or Follow-The-Regularized-Leader and their variants. Particular attention is given to the issue of tuning the parameters of the algorithms and learning in unbounded domains, through adaptive and parameter-free online learning algorithms. Non-convex losses are dealt through convex surrogate losses and through randomization. The bandit setting is also briefly discussed, touching on the problem of adversarial and stochastic multi-armed bandits. These notes do not require prior knowledge of convex analysis and all the required mathematical tools are rigorously explained. Moreover, all the proofs have been carefully chosen to be as simple and as short as possible.