Combinatorial and Algebraic Properties of Nonnegative Matrices

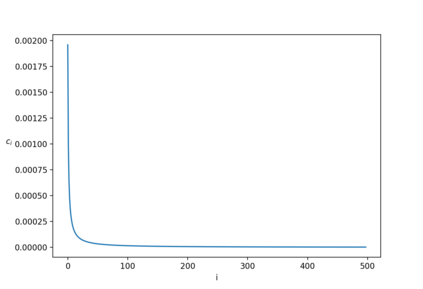
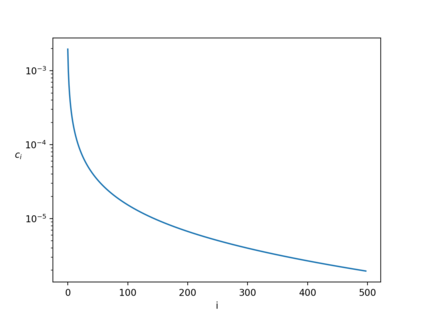
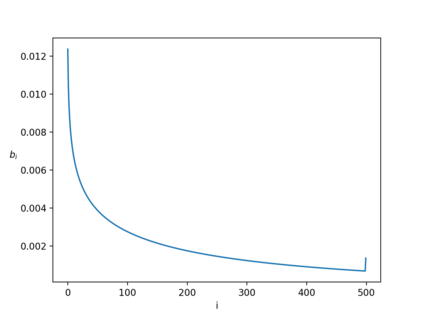
We study the combinatorial and algebraic properties of Nonnegative Matrices. Our results are divided into three different categories. 1. We show a quantitative generalization of the 100 year-old Perron-Frobenius theorem, a fundamental theorem which has been used within diverse areas of mathematics. The Perron-Frobenius theorem states that every irreducible nonnegative matrix $R$ has a largest positive eigenvalue $r$, and every other eigenvalue $\lambda$ of $R$ is such that $\text{Re}\lambda<r$ and $|\lambda|\leq r$. We capture the notion of irreducibility through the widely studied notion of edge expansion $\phi$ of $R$ which intuitively measures how well-connected the underlying digraph of $R$ is, and show a quantitative relation between the spectral gap $\Delta=1-\text{Re}\lambda/r$ (where $\lambda\not=r$ is the eigenvalue of $R$ with the largest real part) and the edge expansion $\phi$, providing a more general result than the Cheeger-Buser inequalities, as follows.\[\dfrac{1}{15}\cdot\dfrac{\Delta(R)}{n}\leq\phi(R)\leq\sqrt{2\cdot\Delta(R)}.\] 2. We study constructions of specific nonsymmetric matrices (or nonreversible Markov Chains) that have small edge expansion but large spectral gap, and provide a novel construction of a nonreversible chain for which\[\phi(R)\leq\dfrac{\Delta(R)}{\sqrt{n}},\] and we also present a candidate construction of matrices for which\[\phi(R)\leq2\dfrac{\Delta(R)}{n},\] which is the most beautiful contribution of this thesis. 3. We connect edge expansion and spectral gap to other combinatorial properties of nonsymmetric matrices, such as mixing time and capacity, and provide elementary proofs or unified views of known results and new results relating the different combinatorial/algebraic properties. Notably, we show the monotonicity of capacity for nonsymmetric nonnegative matrices.