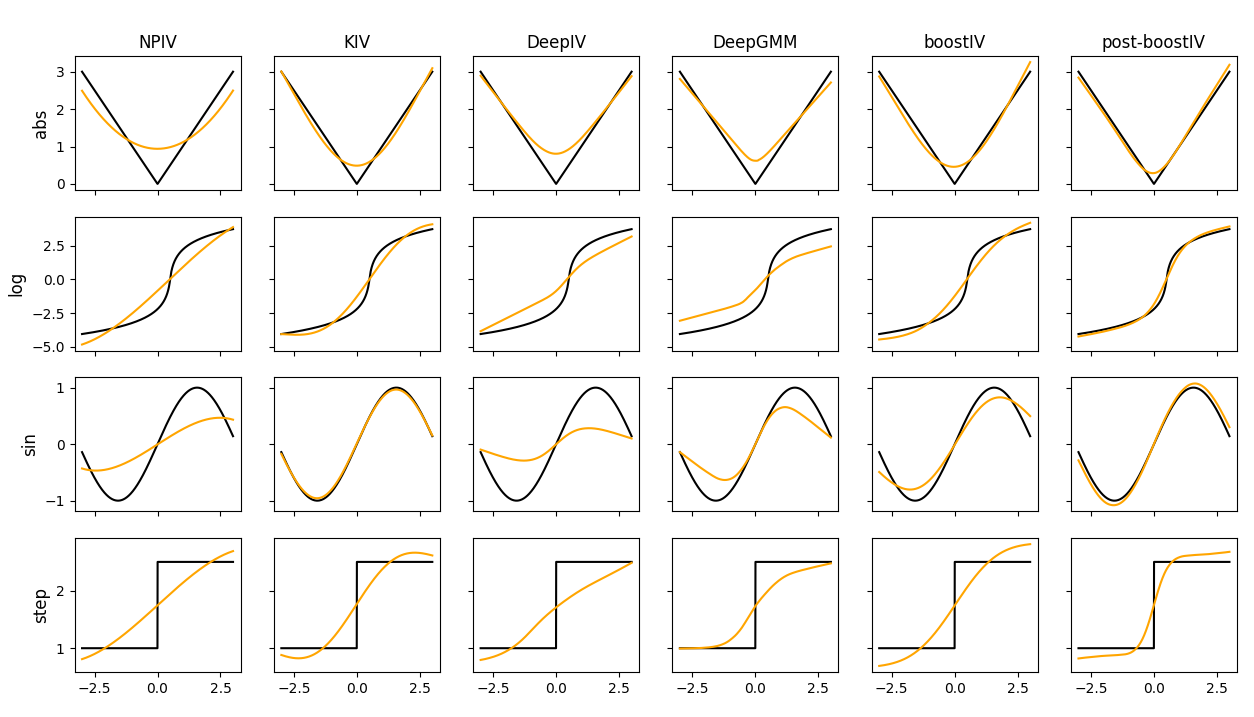
Recent advances in the literature have demonstrated that standard supervised learning algorithms are ill-suited for problems with endogenous explanatory variables. To correct for the endogeneity bias, many variants of nonparameteric instrumental variable regression methods have been developed. In this paper, we propose an alternative algorithm called boostIV that builds on the traditional gradient boosting algorithm and corrects for the endogeneity bias. The algorithm is very intuitive and resembles an iterative version of the standard 2SLS estimator. Moreover, our approach is data driven, meaning that the researcher does not have to make a stance on neither the form of the target function approximation nor the choice of instruments. We demonstrate that our estimator is consistent under mild conditions. We carry out extensive Monte Carlo simulations to demonstrate the finite sample performance of our algorithm compared to other recently developed methods. We show that boostIV is at worst on par with the existing methods and on average significantly outperforms them.
翻译:文献的最近进展表明,标准监督的学习算法不适合本地解释变量的问题。为了纠正内分泌偏差,已经开发出许多非参数工具可变回归法的变种。在本文中,我们提议了一种名为“推进IV”的替代算法,该算法以传统的梯度推进算法为基础,并纠正内分泌偏差。该算法非常直观,类似于标准 2LSSS 估测器的迭代版本。此外,我们的方法是数据驱动的,这意味着研究人员不必对目标函数的近似形式或仪器的选择都表态。我们证明我们的天文图在温和的条件下是一致的。我们进行了广泛的蒙特卡洛模拟,以展示我们算法与其他最近开发的方法相比的有限样本性能。我们显示,推进IV与现有方法相比最差,平均大大超出它们。