Bayesian Over-The-Air Computation

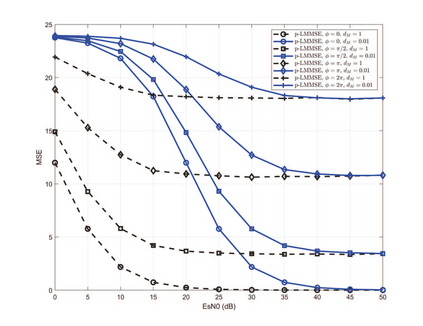
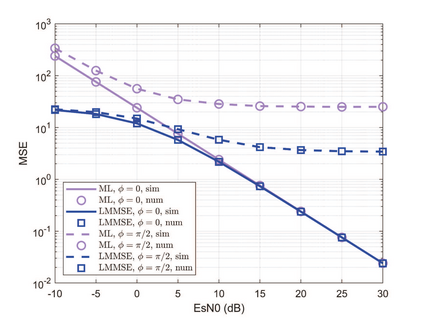
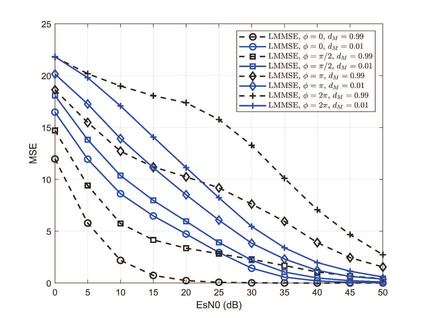
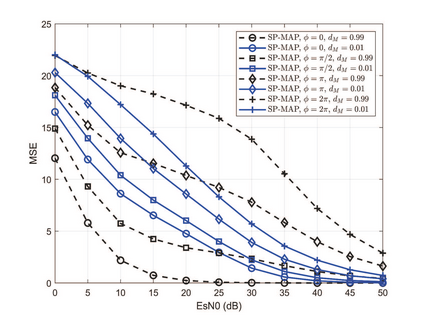
As an important piece of the multi-tier computing architecture for future wireless networks, over-the-air computation (OAC) enables efficient function computation in multiple-access edge computing, where a fusion center aims to compute a function of the data distributed at edge devices. Existing OAC relies exclusively on the maximum likelihood (ML) estimation at the fusion center to recover the arithmetic sum of the transmitted signals from different devices. ML estimation, however, is much susceptible to noise. In particular, in the misaligned OAC where there are channel misalignments among transmitted signals, ML estimation suffers from severe error propagation and noise enhancement. To address these challenges, this paper puts forth a Bayesian approach by letting each edge device transmit two pieces of statistical information to the fusion center such that Bayesian estimators can be devised to tackle the misalignments. Numerical and simulation results verify that, 1) For the aligned and synchronous OAC, our linear minimum mean squared error (LMMSE) estimator significantly outperforms the ML estimator. In the low signal-to-noise ratio (SNR) regime, the LMMSE estimator reduces the mean squared error (MSE) by at least 6 dB; in the high SNR regime, the LMMSE estimator lowers the error floor of MSE by 86.4%; 2) For the asynchronous OAC, our LMMSE and sum-product maximum a posteriori (SP-MAP) estimators are on an equal footing in terms of the MSE performance, and are significantly better than the ML estimator. Moreover, the SP-MAP estimator is computationally efficient, the complexity of which grows linearly with the packet length.