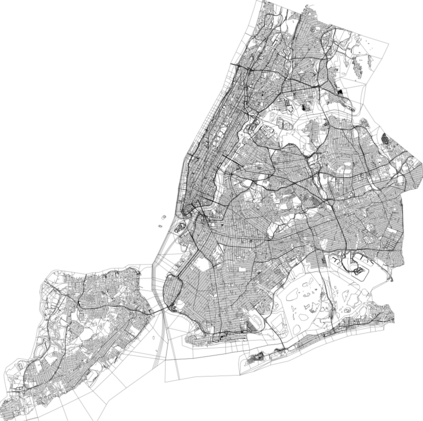
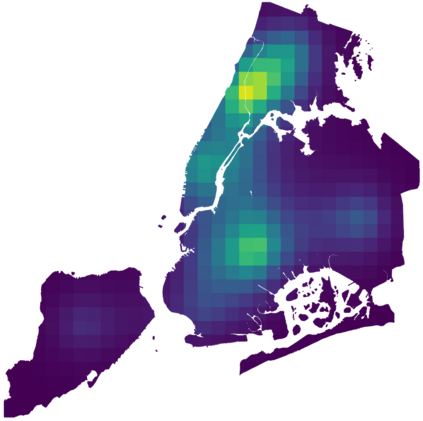
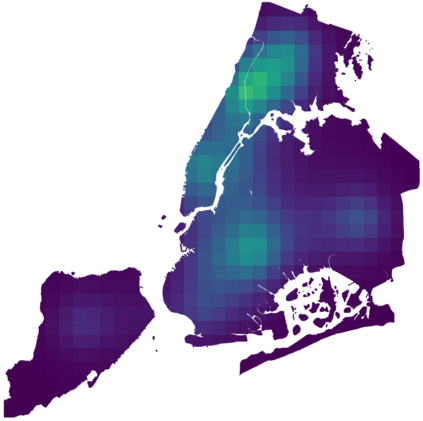
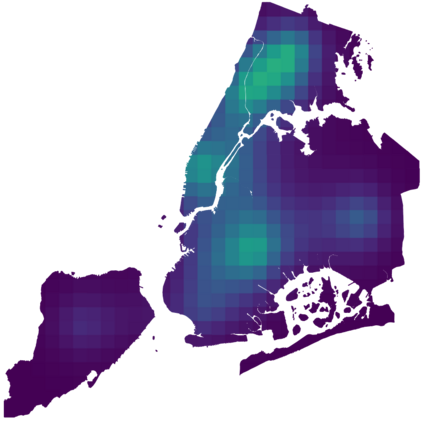
We introduce a scalable approach to Gaussian process inference that combines spatio-temporal filtering with natural gradient variational inference, resulting in a non-conjugate GP method for multivariate data that scales linearly with respect to time. Our natural gradient approach enables application of parallel filtering and smoothing, further reducing the temporal span complexity to be logarithmic in the number of time steps. We derive a sparse approximation that constructs a state-space model over a reduced set of spatial inducing points, and show that for separable Markov kernels the full and sparse cases exactly recover the standard variational GP, whilst exhibiting favourable computational properties. To further improve the spatial scaling we propose a mean-field assumption of independence between spatial locations which, when coupled with sparsity and parallelisation, leads to an efficient and accurate method for large spatio-temporal problems.
翻译:我们引入了一种可伸缩的GP方法,将时空空间过滤与自然梯度变异推法相结合,从而形成一种非兼容的多变量数据GP方法,在时间上以线性衡量。我们的自然梯度方法可以应用平行过滤和平滑,进一步降低时间跨度复杂性,使其在时间步骤数量上具有对数性。我们得出一种稀薄的近似,在一组减少的空间诱导点上构建一个州空间模型,并表明对于塞帕利·马尔科夫内核来说,完整和稀少的病例完全恢复标准变异GP,同时展现出有利的计算特性。为了进一步改善空间空间尺度,我们提出了空间位置之间独立的中位假设,这种假设如果加上宽度和平行性,将会导致一个高效和准确的大型时空问题的方法。