Multi-agent Natural Actor-critic Reinforcement Learning Algorithms

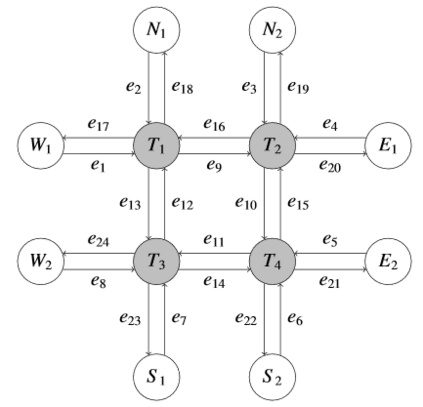
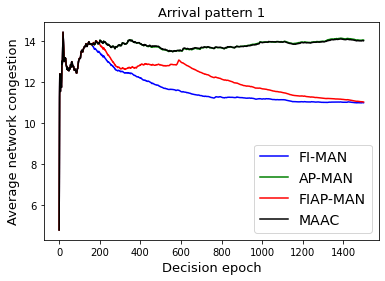
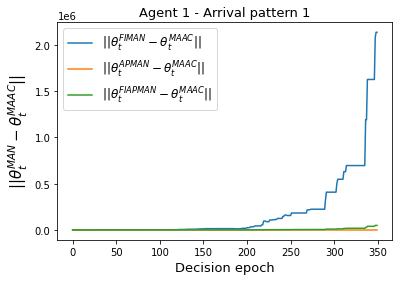
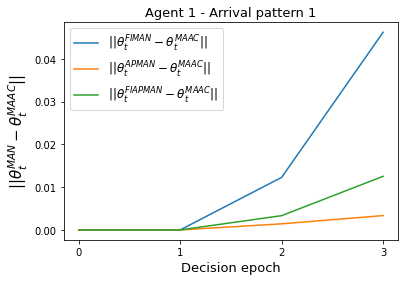
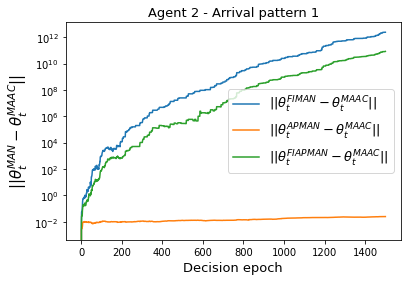
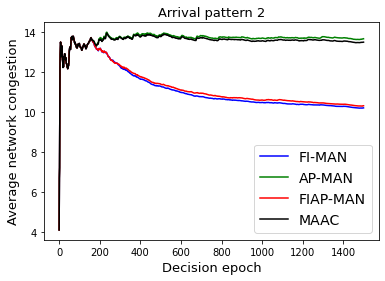
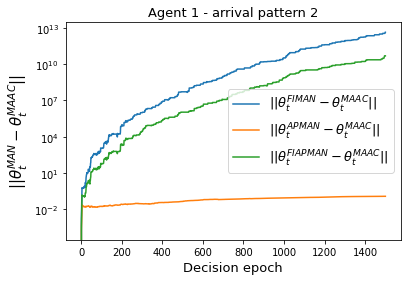
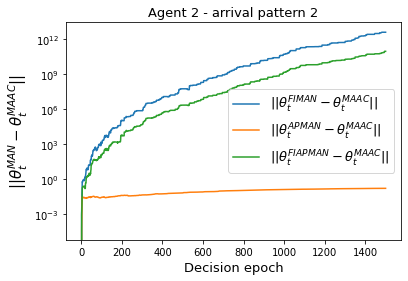
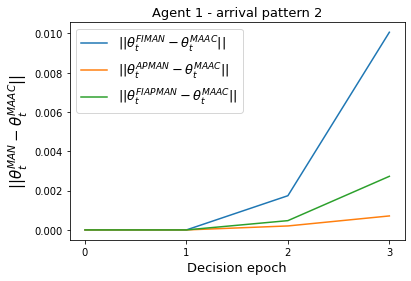
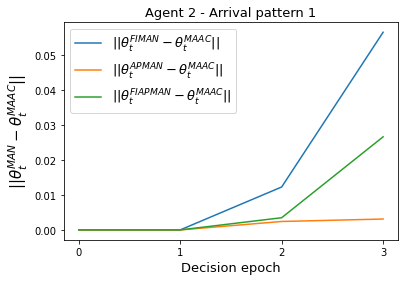
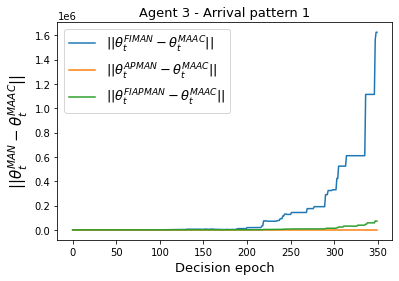
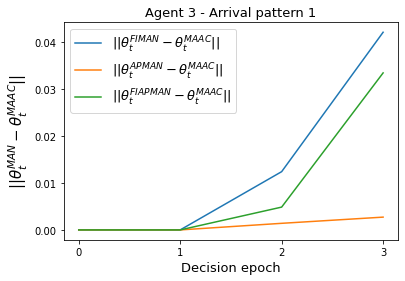
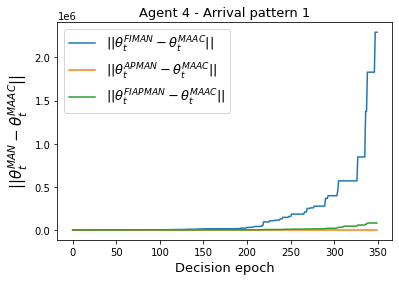
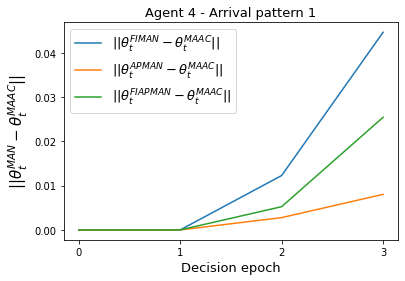
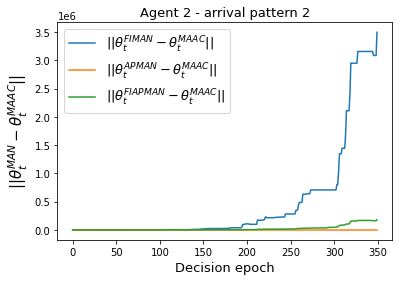
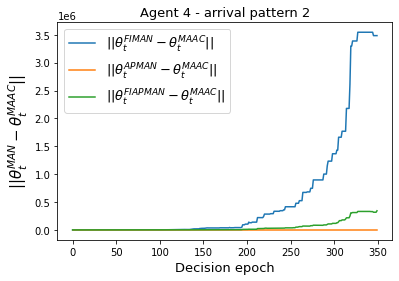
Both single-agent and multi-agent actor-critic algorithms are an important class of Reinforcement Learning algorithms. In this work, we propose three fully decentralized multi-agent natural actor-critic (MAN) algorithms. The agents' objective is to collectively learn a joint policy that maximizes the sum of averaged long-term returns of these agents. In the absence of a central controller, agents communicate the information to their neighbors via a time-varying communication network while preserving privacy. We prove the convergence of all the 3 MAN algorithms to a globally asymptotically stable point of the ODE corresponding to the actor update; these use linear function approximations. We use the Fisher information matrix to obtain the natural gradients. The Fisher information matrix captures the curvature of the Kullback-Leibler (KL) divergence between polices at successive iterates. We also show that the gradient of this KL divergence between policies of successive iterates is proportional to the objective function's gradient. Our MAN algorithms indeed use this \emph{representation} of the objective function's gradient. Under certain conditions on the Fisher information matrix, we prove that at each iterate, the optimal value via MAN algorithms can be better than that of the multi-agent actor-critic (MAAC) algorithm using the standard gradients. To validate the usefulness of our proposed algorithms, we implement all the 3 MAN algorithms on a bi-lane traffic network to reduce the average network congestion. We observe an almost 25% reduction in the average congestion in 2 MAN algorithms; the average congestion in another MAN algorithm is on par with the MAAC algorithm. We also consider a generic 15 agent MARL; the performance of the MAN algorithms is again as good as the MAAC algorithm. We attribute the better performance of the MAN algorithms to their use of the above representation.